Solution March 27, 2007

Let 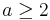$a\geq 2$ be a natural number. Prove that 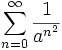$\sum_{n=0}^\infty\frac1{a^{n^{2}}}$ is irrational.

Proof:

Let 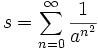$s = \sum_{n=0}^\infty\frac1{a^{n^{2}}}$ .

We use the following result from basic number theory: that for any rational $r$ , and any base $a$ (where 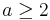$a \ge 2$ is a natural number), the base $a$ expansion of $r$ eventually becomes periodic, i.e. a string of digits eventually is repeated, even if that string is the digit $0$ . (For example, 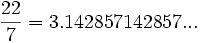$\frac{22}{7} = 3.142857142857...$ in base $10$ .)

Thus, in base $a$ , $s = b 0 . b 1 b 2 b 3 b 4 ... = 1.1001...$ , such that $b k = 1$ if 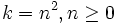$k=n^2, n \ge 0$ and $b k = 0$ otherwise. Suppose $s$ is rational and hence its expansion becomes periodic. Then, since 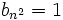$b_{n^2}=1$ for all 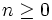$n \ge 0$ , that string of digits must include a $1$ . Suppose it starts at index 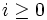$i \ge 0$ and has length 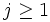$j\ge 1$ . This implies any string of $j$ consecutive digits that starts after $i$ in the expansion must contain a $1$ .

Now, let $n = i + j$ : then $i < n 2 < n 2 + j < (n + 1) 2$ . Since 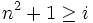$n^2+1 \ge i$ , the digits 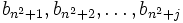$b_{n^2+1},b_{n^2+2},\ldots,b_{n^2+j}$ must contain a $1$ by our earlier observation. But $n 2 < n 2 + 1 < ... < n 2 + j < (n + 1) 2$ implies every digit in that sequence is $0$ , a contradiction, and hence $s$ can't be rational. $\square$

Retrieved from "http://www.efnet-math.org/w/Solution_March_27%2C_2007"