Solution March 27a, 2007
Problem
Prove that for each 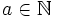 , there are infinitely many natural
, there are infinitely many natural  , such that
, such that
Solution
Fix 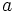 and let p > a be a prime. Let
and let p > a be a prime. Let 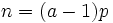 .
We will show that
.
We will show that  satisfies (1).
satisfies (1).
Let 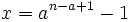 . Because
. Because 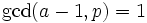 , we just need to show that
, we just need to show that 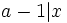 and
and 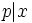 .
.
Modulo 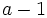 we have
we have 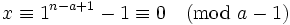 , while modulo
, while modulo 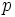 ,
, 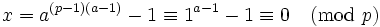 , using Fermat's little Theorem (http://en.wikipedia.org/wiki/Fermat's_little_theorem).
, using Fermat's little Theorem (http://en.wikipedia.org/wiki/Fermat's_little_theorem).
Because there are infinitely many primes, we can construct infinitely many solutions to (1) for a given 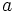 this way, completing the proof.
this way, completing the proof.