Solution March 3, 2007
Prove that there exist no 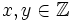 such that
such that 
Proof suggested by landen based on Rose, A Course in Number Theory. Proof by int-e.
This problem is a special case of the following theorem.
 has no solutions in two cases:
has no solutions in two cases:
-
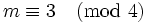 ,
,  is even, and
is even, and 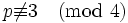 when
when 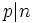
-
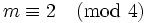 ,
,  is odd, and
is odd, and 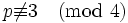 when
when 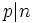
The problem of the day is an instance of case 1, because 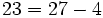 .
.
Proof.
Assume we have a solution.
In both cases, 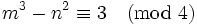 . If
. If  is even, we have
is even, we have 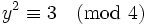 , a contradiction. So
, a contradiction. So  is odd and
is odd and 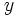 is even. It follows that
is even. It follows that 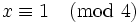 .
.
We can rewrite the equation as  .
Both factors are non-negative;
.
Both factors are non-negative; 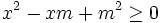 is true for all
is true for all  , while
, while 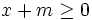 follows from
follows from 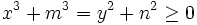 .
.
In case 1, 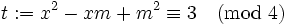 , so
, so 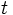 has a prime divisor
has a prime divisor 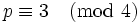 . Modulo
. Modulo 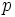 , we have
, we have 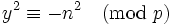 .
. 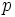 can not divide
can not divide  because that would violate the conditions for
because that would violate the conditions for  so we can divide by
so we can divide by 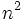 . We find that
. We find that 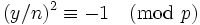 , which is a contradiction because
, which is a contradiction because 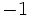 is not a quadratic residue (http://en.wikipedia.org/wiki/Quadratic_residue) modulo
is not a quadratic residue (http://en.wikipedia.org/wiki/Quadratic_residue) modulo 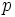 .
.
In case 2,  and we get a contradiction in the same way.
and we get a contradiction in the same way. 