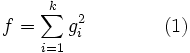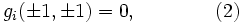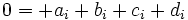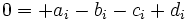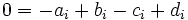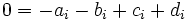Solution March 30, 2007

Problem

Let 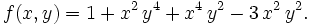$f(x,y) = 1 + x^{2}\,y^{4}+x^{4}\,y^{2}-3\,x^{2}\,y^{2}.$

Determine whether there exist polynomials $g i (x, y)$ with real coefficients such that

$f = \sum_{i=1}^{k}g_{i}^{2}\qquad\qquad(1)$

or argue that such a representation is not possible.

Solution

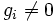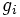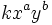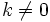We will have to resort to arguing. Assume without loss of generality that $g_i\neq 0$ . Let $g_i\,$ be fully expanded to sums of terms of the form $k x^ay^b\,$ with $k\neq0$ .

Note that 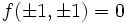$f(\pm1,\pm1) = 0$ , so

$g_i(\pm1, \pm1) = 0,\qquad\qquad(2)$

because a sum of squares of real numbers is zero if and only if all the numbers are zero.

If 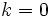$k=0\,$ we'd have 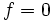$f=0\,$ . So $k>0\,$ .

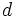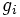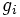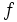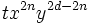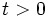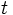Let $d\,$ be the maximum degree of the $g_i\,$ . Pick the smallest $n\,$ such that there is a term $k x^ny^{d-n}\,$ in one of the $g_i\,$ . Then, by comparing coefficients in (1), we find that $f\,$ contains a term of the form $tx^{2n}y^{2d-2n}\,$ with $t>0\,$ ( $t\,$ is the sum of at least one non-zero square, and thus positive), so 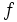$f\,$ has degree at least $2d\,$ .

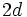Therefore, the degree of 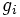$g_i\,$ is at most 3.

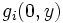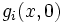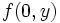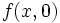By a similar argument, $g_i(0,y)\,$ and $g_i(x,0)\,$ must be constant, because $f(0,y)\,$ and $f(x,0)\,$ are constant polynomials.

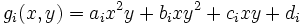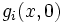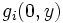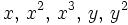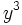This means that $g_i(x,y) = a_ix^2y + b_ixy^2 + c_ixy + d_i\,$ (what we just said about $g_i(x,0)\,$ and $g_i(0,y)\,$ means that the coefficients for $x,\,x^2,\,x^3,\,y,\,y^2$ and $y^3\,$ are zero) for some real numbers 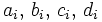$a_i,\,b_i,\,c_i,\,d_i$ . (2) is then equivalent to the following system of linear equations:

$0 = + a_i + b_i + c_i + d_i\,$

$0 = + a_i - b_i - c_i + d_i\,$

$0 = - a_i + b_i - c_i + d_i\,$

$0 = - a_i - b_i + c_i + d_i\,$

Solving these we find $g_i = 0\,$ , contradicting our assumptions.

Retrieved from "http://www.efnet-math.org/w/Solution_March_30%2C_2007"