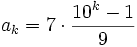Solution May 22, 2007
Problem
Prove or disprove:
For any positive integer  there is a positive integer
there is a positive integer  such that
such that 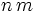 has only 0's and 7's as decimal digits.
has only 0's and 7's as decimal digits.
Solution
This is true.
Consider the sequence 7, 77, 777, etc, formally
modulo  . This is an infinite sequence but there are only finitely many (namely,
. This is an infinite sequence but there are only finitely many (namely,  ) residues modulo
) residues modulo  so let
so let
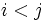 be chosen such that
be chosen such that 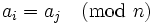 .
.
Then, the difference 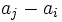 is divisible by
is divisible by  .
Its decimal digits form a sequence of 7s followed by 0s, so
.
Its decimal digits form a sequence of 7s followed by 0s, so 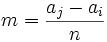 satisfies all requirements of the problem.
satisfies all requirements of the problem.