Solution Nov. 22, 2006

For a positive rational 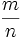$\frac{m}{n}$ define

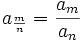
$a_{\frac{m}{n}} = \frac{a_m}{a_n}$

This is well defined because

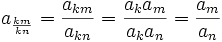
$a_{\frac{km}{kn}} = \frac{a_{km}}{a_{kn}} = \frac{a_k a_m}{a_k a_n} = \frac{a_m}{a_n}$

It's similarly easy to show that it's monotonic and multiplicative.

For a positive real x define

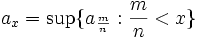
$a_x = \sup \{ a_{\frac{m}{n}} : \frac{m}{n} < x \}$

It's again easy to show that 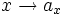$x \to a_x$ is monotonic and multiplicative.

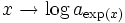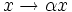
Now, $x \to \log a_{\exp(x)}$ is monotone and additive, so by a standard theorem (which is easy to prove - it's obvious for rational x and then follows for real x by continuity) is of the form $x \to \alpha x$

Hence $a n = e x p (αlog n) = n α$ as desired.

Retrieved from "http://www.efnet-math.org/w/Solution_Nov._22%2C_2006"