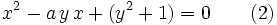Solution Nov. 30, 2006
Solution by int-e. Editing by landen.
Let  and
and 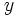 be positive integers such that
be positive integers such that 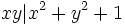 . Show that
. Show that 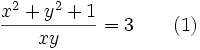
This is equivalent to a quadratic equation in  with
with 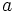 being the quotient. We want to show that
being the quotient. We want to show that 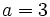 :
:
Holding 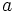 fixed there is a pair
fixed there is a pair 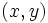 with
with 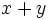 as small as possible. By symmetry we can take
as small as possible. By symmetry we can take 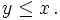
The quadratic in  has the product of its roots
has the product of its roots 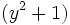 . This means that
. This means that 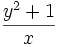 is also in a solution
is also in a solution 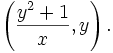
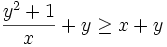 by the minimality of
by the minimality of 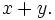
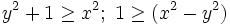 has the only solution
has the only solution 
Then putting 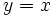 in (2) gives:
in (2) gives:
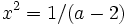 which has the solution
which has the solution  and
and