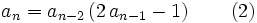Solution November 11, 2006

1. 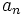$a_{n}\,$ is a sequence that 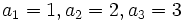$a_{1}=1,a_{2}=2,a_{3}=3\,$ , and

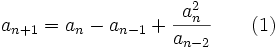$a_{n+1}=a_{n}-a_{n-1}+\frac{a_{n}^{2}}{a_{n-2}}\qquad (1)$ Prove that for each natural 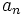$n\,$ , $a_{n}\,$ is integer.

Not every good solution by landen. I don't know any real organized way to find how to do it.

If we conjecture that 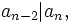$a_{n-2} | a_{n},\,$ then look at what would be a nice other factor, we conjecture that:

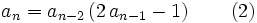$a_{n}=a_{n-2}\left( 2\,a_{n-1}-1\right) \qquad(2)$ Examining a few numbers helps to guess this.

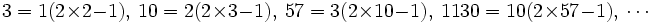
$3=1(2\times 2-1),\ 10=2(2\times 3-1),\ 57=3(2\times 10-1),\ 1130 = 10(2\times 57-1),\ \cdots$

Now we do induction on 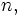$n,\,$ by replacing one 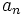$a_{n}\,$ in $(1)\,$ by our induction hypothesis $(2)\,.$

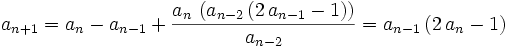
$a_{n+1}=a_{n}-a_{n-1}+\frac{a_{n}\,\left( a_{n-2}\left( 2\,a_{n-1}-1\right) \right)}{a_{n-2}}=a_{n-1}\left( 2\,a_{n}-1\right)$

Which establishes 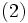$(2)\,$ by induction. $\qquad \square$

Polytope found a solution by a different path.

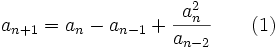
$a_{n+1}=a_{n}-a_{n-1}+\frac{a_{n}^{2}}{a_{n-2}}\qquad (1)$

Can be rearranged to:

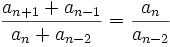
$\frac{a_{n+1}+a_{n-1}}{a_{n}+a_{n-2}} = \frac{a_{n}}{a_{n-2}}$

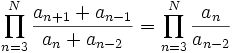
Next taking the products of boths sides: $\prod_{n=3}^N\frac{a_{n+1}+a_{n-1}}{a_{n}+a_{n-2}} = \prod_{n=3}^N\frac{a_{n}}{a_{n-2}}$

There is awesome cancellation in both telescoping products leaving after rearrangement: $a_{n}=a_{n-2}\left( 2\,a_{n-1}-1\right) \qquad(2)$
$\square$