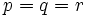Solution Problem 3, Dec 16, 2006

Let a, b, c be the lengths of the sides of a triangle. Prove that

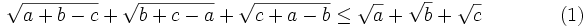
$\sqrt{a+b-c} + \sqrt{b+c-a} + \sqrt{c+a-b} \leq \sqrt{a} + \sqrt{b} + \sqrt{c}\qquad\qquad (1)$

and determine when equality occurs.

Proof:

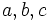$a,b,c\,$ have to satisfy the triangle inequality, e.g., 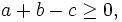$a+b-c\ge 0,\,$ etc. One way to handle this is to define new variables with a simpler constraint.

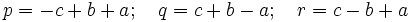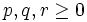
$p=-c+b+a;\quad q=c+b-a;\quad r=c-b+a$ with $p,q,r \ge 0\,$

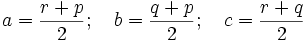
$a={{r+p}\over{2}};\quad b={{q+p}\over{2}};\quad c={{r+q}\over{2}}$

In these variables:
$\sqrt{p}+\sqrt{q}+\sqrt{r} \leq \sqrt{{{r+p}\over{2}}} + \sqrt{{{q+p}\over{2}}}+\sqrt{{{r+q}\over{2}}}\qquad\qquad(2)$

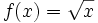$f(x)=\sqrt{x}$ is a strictly concave function because the second derivative is negative. Using Jensen's inequality (http://planetmath.org/encyclopedia/JensensInequality.html), we have:
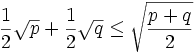$\frac{1}{2}\sqrt{p} + \frac{1}{2}\sqrt{q}\leq \sqrt{\frac{p+q}{2}}$ with equality requiring $p=q.\,\qquad\qquad(3)$

When we sum (3) for the other cases (2) is proven.

If any one of the inequalities (3) is strictly not equal then (2) is strictly not equal, so equality requires $p=q=r\,$

$\square\,$

Retrieved from "http://www.efnet-math.org/w/Solution_Problem_3%2C_Dec_16%2C_2006"