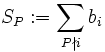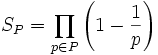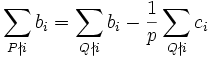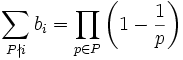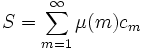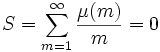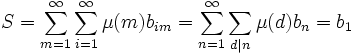Solution September 20, 2007

Problem

Does there exist a sequence 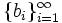$\{b_{i}\}_{i=1}^\infty$ of positive real numbers such that for each natural m: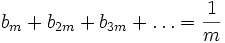 $b_{m}+b_{2m}+b_{3m}+\dots=\frac1m$

Solution

Assume that there is such a sequence $(b i)$ .

Let $P$ be a set of prime numbers. Say that $P$ divides $n$ (symbolically, $P | n$ ) if any member of $P$ divides $n$ .

Define

$S_P�:= \sum_{P \nmid i}b_i$

$S P$ is well-defined because it sums a subsequence of $(b i)$ and all $b i$ are positive.

Lemma: If $P$ is finite, then

$S_P = \prod_{p \in P} \left(1-\frac1p\right)$

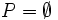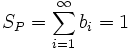Proof: By induction on the size of $P$ . If $P=\empty$ then $S_P = \sum_{i=1}^\infty b_i = 1$ .

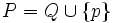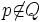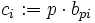Now let $P = Q \cup\{p\}$ with $p\not\in Q$ . Consider the sequence $c_i�:= p\cdot b_{pi}$ . It satisfies all requirements of $(b i)$ . Therefore,

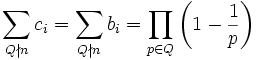$\sum_{Q\nmid n}c_i = \sum_{Q\nmid n} b_i = \prod_{p \in Q} \left(1-\frac1p\right)$ .

A number $n$ satisfies 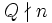$Q\nmid n$ if either 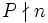$P\nmid n$ or $p | n$ and 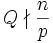$Q\nmid \frac np$ . So

$\sum_{P\nmid i} b_i = \sum_{Q\nmid i} b_i - \frac1p\sum_{Q\nmid i} c_i$

and we get

$\sum_{P\nmid i} b_i = \prod_{p \in P} \left(1-\frac1p\right)$

This completes the induction step and thus proves the lemma.

Let 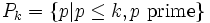$P_k = \{p | p \leq k, p \mathrm{\ prime}\}$ .

Because 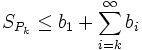$S_{P_k} \leq b_1 + \sum_{i=k}^\infty b_i$ we have that

$\lim_{k\to\infty}S_{P_k} = b_1$

Therefore,

$b_1 = \prod_{p \mathrm{\ prime}}\left(1-\frac1p\right) = 0$

which is not positive. Thus no sequence $(b i)$ satisfying the problem's requirements exists.

Note: By considering 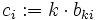$c_i�:= k\cdot b_{ki}$ we can show that $b k = 0$ for all $k$ . So the answer does not change if we replace "positive" by "nonnegative".

Short "proof"

This "proof" makes use of the Möbius function (http://mathworld.wolfram.com/MoebiusFunction.html).

Assume there is such a sequence $(b i)$ . Let 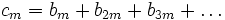$c_m = b_{m}+b_{2m}+b_{3m}+\dots$

Consider the sum

$S = \sum_{m=1}^\infty \mu(m)c_{m}$

Now on the one hand,

$S = \sum_{m=1}^\infty \frac{\mu(m)}m = 0$

On the other hand,

$S = \sum_{m=1}^\infty\sum_{i=1}^\infty \mu(m)b_{im} = \sum_{n=1}^\infty\sum_{d|n}\mu(d)b_{n} = b_1\,$

So $b 1 = 0$ which doesn't satisfy the requirements of the problem.

Retrieved from "https://www.efnet-math.org:443/w/Solution_September_20%2C_2007"