Solution Tuesday, February 20, 2007

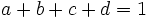Let $a,b,c,d\,$ be positive real numbers such that $a+b+c+d=1\,$ . Prove that

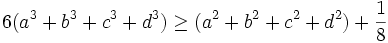
$6(a^3+b^3+c^3+d^3)\ge(a^2+b^2+c^2+d^2)+\frac{1}{8}\,$

Solution by landen

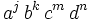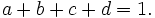This is a standard type of inequality. It can be done by a brute force method. The first step is to "homogenize" the inequality. We want the situation such that all terms of the form $a^j\,b^k\,c^m\,d^n$ have $j+k+m+n=3.\,$ We do this by multiplying terms by appropriate powers of $a+b+c+d=1.\,$ We want to prove:

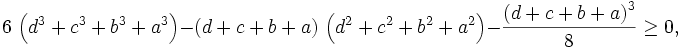$6\,\left(d^3+c^3+b^3+a^3\right)-\left(d+c+b+a\right)\,\left(d^2+c^2 +b^2+a^2\right)-{{\left(d+c+b+a\right)^3}\over{8}}\geq 0,$ expanding and multiplying by 8:

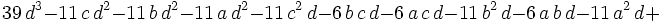
$39\,d^3-11\,c\,d^2-11\,b\,d^2-11\,a\,d^2-11\,c^2\,d-6\,b\,c\,d-6\,a \,c\,d-11\,b^2\,d-6\,a\,b\,d-11\,a^2\,d+$
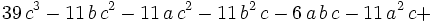
$39\,c^3-11\,b\,c^2-11\,a\,c^2 -11\,b^2\,c-6\,a\,b\,c-11\,a^2\,c+$
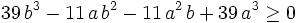
$39\,b^3-11\,a\,b^2-11\,a^2\,b+39\, a^3\geq 0$

This is more friendly than it looks. Since the sums of the exponents are constant, we can apply "bunching" or Muirhead's inequality. (http://planetmath.org/encyclopedia/MuirheadsInequality.html)

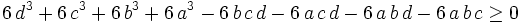$6\,d^3+6\,c^3+6\,b^3+6\,a^3 -6\,b\,c\,d-6\,a\,c\,d-6\,a\,b\,d-6\,a\,b\,c\geq 0$ from $s=[0,0,0,3]\,$ and $t=[0,1,1,1]\,$ in Muirhead's inequality. (http://planetmath.org/encyclopedia/MuirheadsInequality.html) Also:

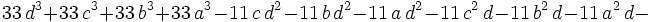
$33\,d^3+33\,c^3+33\,b^3+33\,a^3 -11\,c\,d^2-11\,b\,d^2-11\,a\,d^2-11\,c^2\,d-11\,b^2\,d-11\,a^2\,d-$
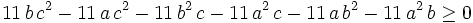$11 \,b\,c^2-11\,a\,c^2-11\,b^2\,c-11\,a^2\,c-11\,a\,b^2-11\,a^2\,b\geq 0$ from $s=[0,0,0,3]\,$ and $t=[0,0,1,2]\,$

Adding these two inequalities we establish the main inequality.

$\square$

Retrieved from "http://www.efnet-math.org/w/Solution_Tuesday%2C_February_20%2C_2007"