Solution for January 6, 2007
Find all natural numbers 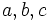 greater than one such that
greater than one such that 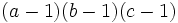 divides
divides 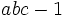 exactly.
exactly.
Proof by landen
I couldn't find a nice hand proof so I used the computer to help.
First result was that 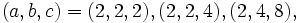 or
or 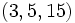 are the only solutions for
are the only solutions for 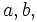 and
and 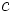 all less than
all less than 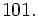
Let 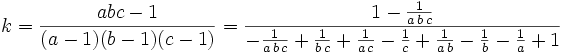
If 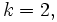 then
then 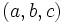 are all odd and
are all odd and 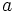 is at least
is at least 
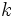 is decreasing as
is decreasing as 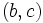 increase. So for
increase. So for 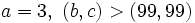 we have
we have
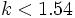 which is a contradiction. So for
which is a contradiction. So for 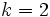 the only solution is
the only solution is 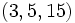
If 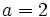 or
or 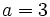 we have
we have 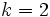 for additional solutions by numerical calculation.
for additional solutions by numerical calculation.
If 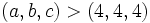 then
then 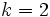 for additional solutions.
for additional solutions.
Since all 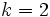 solutions are known there are no others.
solutions are known there are no others.
