Solution for November 5, 2006

Evaluate:

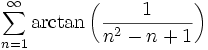
$\sum_{n=1}^{\infty }{\arctan \left({{1}\over{n^2-n+1}}\right)}$

Proof I by landen

We can derive a trig identity by differentiating and then integrating.

${{d}\over{d\,n}}\,\arctan \left({{1}\over{n^2-n+1}}\right) = -{{2\,n-1}\over{\left(n^2+1\right)\,\left(n^2-2\,n+2\right)}} = {{1}\over{n^2+1}}-{{1}\over{\left(n-1\right)^2+1}}$

If we integrate both sides, and check at 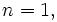$n=1,\,$ that the constant of integration is 0 we get the trig identity:

$\arctan \left({{1}\over{n^2-n+1}}\right)=\arctan n-\arctan \left(n- 1\right)$ Did you already know this one?

$\sum_{n=1}^{m}{\arctan n-\arctan \left(n-1\right)}=\arctan m$ by telescoping.

$\sum_{n=1}^{\infty }{\arctan \left({{1}\over{n^2-n+1}}\right)} = \lim_{m\rightarrow \infty }{\arctan m}={{\pi}\over{2}}$

$\square$

Proof II by int-e

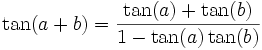
Recall that $\tan(a+b) = \frac{\tan(a)+\tan(b)}{1 - \tan(a)\tan(b)}\,$

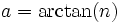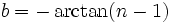Let $a=\arctan(n)\,$ and $b=-\arctan(n-1)\,$ , and apply $\arctan\,$ on both sides. We get $\arctan{n}-\arctan{(n-1)} = \arctan{\frac{1}{1-n+n^2}} \,$

Next telescope as above. $\square$

Retrieved from "http://www.efnet-math.org/w/Solution_for_November_5%2C_2006"