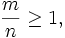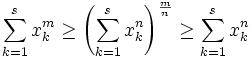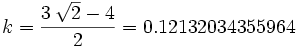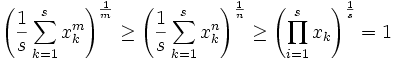Solution for Oct. 13, 2006

Find the biggest real number 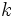$k\,$ that for each right-angled triangle with sides $a,b,c\,$ :

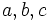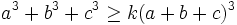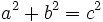
$a^{3}+b^{3}+c^{3}\geq k(a+b+c)^{3}$ ; $a^2+b^2=c^2\,$

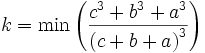
$k = \min \left({{c^3+b^3+a^3}\over{\left(c+b+a\right)^3}}\right)$

Let 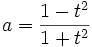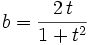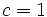$a=\frac{1-t^2}{1+t^2}$ ; $b=\frac{2\,t}{1+t^2}$ ; $c=1\,$ This is justified because the expression to be minimized and the constraint are homogeneous.

We want to minimize 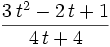${{3\,t^2-2\,t+1}\over{4\,t+4}}$ . Taking the derivative and setting to 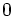$0\,$ we get: 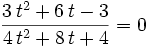${{3\,t^2+6\,t-3}\over{4\,t^2+8\,t+4}}=0$ This has a single positive root at: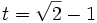 $t=\sqrt{2}-1\,$

$k={{3\,\sqrt{2}-4}\over{2}} =0.12132034355964$

$\square$

II.

For positive numbers 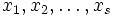$x_{1},x_{2},\dots,x_{s}$ , we know that 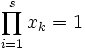$\prod_{i=1}^{s}x_{k}=1$ . Prove that for each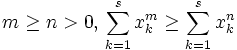 $m\geq n>0,\, \sum_{k=1}^{s}x_{k}^{m}\geq\sum_{k=1}^{s}x_{k}^{n}$

Using the generalized power mean, (http://en.wikipedia.org/wiki/Generalized_mean) we have:

$\left( \frac{1}{s}\sum_{k=1}^{s}x_{k}^{m}\right)^\frac{1}{m}\geq \left( \frac{1}{s}\sum_{k=1}^{s}x_{k}^{n}\right)^\frac{1}{n}\geq \left( \prod_{i=1}^{s}x_{k}\right )^\frac{1}{s}=1$

Raising to the $m\,$ th power and multiplying by $s$ .

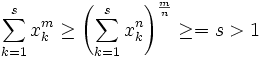
$\sum_{k=1}^{s}x_{k}^{m}\geq \left( \sum_{k=1}^{s}x_{k}^{n}\right)^\frac{m}{n}\geq= s> 1$

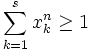$\sum_{k=1}^{s}x_{k}^{n}\geq 1$ follows and since $\frac{m}{n}\geq 1,\,$

$\sum_{k=1}^{s}x_{k}^{m}\geq \left( \sum_{k=1}^{s}x_{k}^{n}\right)^\frac{m}{n}\geq \sum_{k=1}^{s}x_{k}^{n}$

$\square$

Retrieved from "http://www.efnet-math.org/w/Solution_for_Oct._13%2C_2006"