Solution for Oct. 14, 2006

This result, known as the Erdös-Szekeres Theorem (one of two under that name), dates back to a 1935 paper of Erdös and Szekeres that marked a rediscovery of Ramsey's Theorem (1930) and began the study of Ramsey Theory. This proof, which is due to Hammersley, is not the original, but it's a cute little constructive proof, reproduced from Steele's "Probability Theory and Combinatorial Optimization":

Treat the sequence as a pile of numbered checkers, where $a i$ is the number on the $i$ th checker. Construct new piles as follows:

1. Let $a 1$ start the first pile.

2. For each subsequent $i$ , place checker $a i$ on the first pile for which $a i$ is larger than the checker on top; if there is none, start a new pile.

At the end, as there are $r s + 1$ checkers, some pile has at least $r + 1$ checkers; otherwise there are at least $s + 1$ piles by the pigeonhole principle (as at most $s$ piles of at most $r$ checkers each implies at most $r s$ checkers).

In the former case, any pile with at least $r + 1$ checkers forms an increasing subsequence directly from the algorithm. In the latter case, by noting that each time we place a checker $a i$ in the $k$ th pile (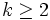 $k \ge 2$ ), there is a checker $a j$ in the $(k - 1)$ st pile pile with $j < i$ and $a j > a i$ , we can therefore form a decreasing sequence whose length is the number of piles. $\square$

Retrieved from "http://www.efnet-math.org/w/Solution_for_Oct._14%2C_2006"