Solution for Oct. 31, 2006

Show 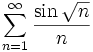$\sum_{n=1}^{\infty }{{{\sin \sqrt{n}}\over{n}}}$ converges.

Overview

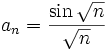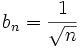
Let $a_n = {{{\sin \sqrt{n}}\over{\sqrt{n}}}}$ ; $b_n= {{1}\over{\sqrt{n}}}$

The plan is to show that the partial sums

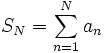$S_N =\sum_{n=1}^{N }a_n$ are bounded.

Then 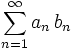$\sum_{n=1}^{\infty }{a_n\, b_n}$ converges by Abel's test. (http://pirate.shu.edu/projects/reals/numser/t_abel.html)

Using some experience we can guess a symmetric difference that will have our summand in its Taylor series. The integral of the summand always works but often we can guess a difference that produces the desired term without an analytic integral. Using Taylor's theorem about $n\,$ with the Lagrange form (http://en.wikipedia.org/wiki/Taylor's_theorem) of the remainder we get:

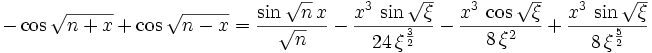
$-\cos \sqrt{n+x}+\cos \sqrt{n-x}={{\sin \sqrt{n}\,x}\over{\sqrt{n}}}-{{x^3\,\sin \sqrt{\xi}}\over{24\,\xi^{{{3}\over{2}}}}}-{{x^3\, \cos \sqrt{\xi}}\over{8\,\xi^2}}+{{x^3\,\sin \sqrt{\xi}}\over{8\,\xi ^{{{5}\over{2}}}}}$

$\xi \in [n-x,n+x]$

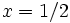Taking $x=1/2\,$ , summing both sides, and using worst case values $\xi=n-1/2\,$ and the $\mbox{trig functions} = 1,\,$ we get:

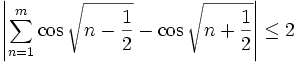
$\left| \sum_{n=1}^{m}{\cos \sqrt{n-{{1}\over{2}}}-\cos \sqrt{n+{{1 }\over{2}}}}\right| \leq 2$

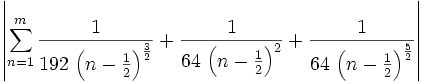$\left| \sum_{n=1}^{m}{{{1}\over{192\,\left(n-{{1}\over{2}}\right)^{ {{3}\over{2}}}}}+{{1}\over{64\,\left(n-{{1}\over{2}}\right)^2}}+{{1 }\over{64\,\left(n-{{1}\over{2}}\right)^{{{5}\over{2}}}}}}\right|$ converges absolutely. Therefore:

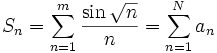$S_n = \sum_{n=1}^{m}{{{\sin \sqrt{n}}\over{n}}}=\sum_{n=1}^{N }a_n$ is bounded.

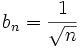$b_n= {{1}\over{\sqrt{n}}}$ goes monotonically to 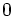$0\,$ as $n\rightarrow \infty\,$

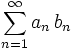Then $\sum_{n=1}^{\infty }{a_n\, b_n}$ converges by Abel's test. (http://pirate.shu.edu/projects/reals/numser/t_abel.html)

$\square$

Retrieved from "http://www.efnet-math.org/w/Solution_for_Oct._31%2C_2006"