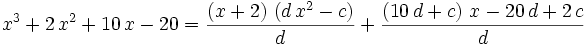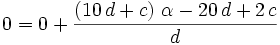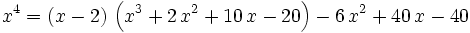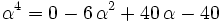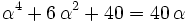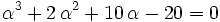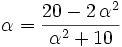Solution for October 11, 2006
 is a real root of
is a real root of 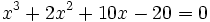 . Show that
. Show that 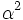 is irrational.
is irrational.
Easy Theory Solution by landen
By the rational roots theorem any rational root of this is an integer divisor of 20. We can check them all and none work.
Another possibility is to find the derivative of the cubic and
notice it is always positive. So there is only 1 real root. Then we
notice the polynomial is negative at  and positive at
and positive at 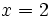 , so the root is not an integer and is therefore irrational.
, so the root is not an integer and is therefore irrational.
Now we have that 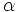 is irrational which is certainly required for the proposition to be true.
is irrational which is certainly required for the proposition to be true.
Assume 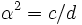 is rational with
is rational with 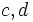 integers.
So we now have that
integers.
So we now have that 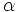 is a root of
is a root of 
Now comes the major tactic. We use polynomial division to find that:
If we substitute 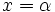 we get:
we get:
This gives that 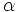 is rational which is a contradiction so that the hypothesis that
is rational which is a contradiction so that the hypothesis that 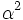 is rational is false.
is rational is false.

Easy Theory Solution by Polytope
Establish that 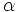 is irrational as above. Next use polynomial division to get:
is irrational as above. Next use polynomial division to get:
If we substitute 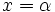 we get:
we get:
If α2 were rational then the left side of the equation is rational and the right side is irrational, which would be a contradiction.

Really Easy Theory Solution by landen
By the rational roots theorem any rational root of this is an integer divisor of 20. We can check them all and none work.
This says 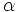 is rational if
is rational if 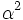 is rational which is a contradiction. So
is rational which is a contradiction. So 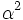 is irrational.
is irrational.

Solution using CAS
The real root of 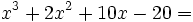
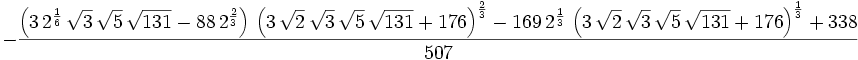
Then 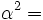
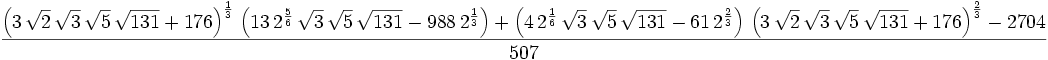
Next we "guess" that 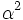 solves the equation:
solves the equation:
Polytope and landen used Maple and Maxima to show that 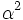 is a root.
is a root.
Next, 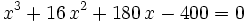 has no rational roots by the rational roots theorem. Therefore,
has no rational roots by the rational roots theorem. Therefore, 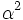 is irrational.
is irrational.