Solutions for Dec. 30, 2006

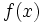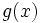$f(x)\,$ and $g(x)\,$ are real valued functions defined on all of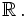 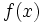$\mathbb{R}\,.$ $f(x)\,$ is not always 0.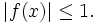 $|f(x)|\leq1.\,$

For all 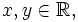$x,y\in \mathbb{R},\,$ $f(x+y)+f(x-y)=2\,f(x)\,g(y).$

Show that 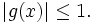$|g(x)|\leq 1.$

Solution by i_c-Y

Since 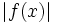$|f(x)|\,$ is bounded it has a least upper bound(lub) which we can call 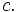$c.\,$ This follows from an axiom for the real numbers. (http://planetmath.org/?op=getobj&from=objects&name=InfimumAndSupremumForRealNumbers) 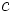$c\,$ is positive because 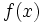$f(x)\,$ is not always zero.

As a premise for contradiction we assume that there is some fixed 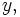$y,\,$ such that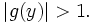 $|g(y)|>1.\,$

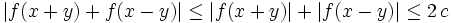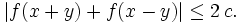
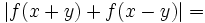$|f(x+y)+f(x-y)| \leq |f(x+y)|+|f(x-y)| \leq 2\,c$ by the triangle inequality. Therefore the lub of $|f(x+y)+f(x-y)| \leq 2\,c.$

The lub of $|f(x+y)+f(x-y)| =\,$ the lub of $2\,|f(x)|\,|g(y)|=2\,c\,|g(y)|\leq 2\,c$

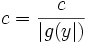$c=\frac{c}{|g(y|)}\,$ This contradicts our assumption that there is a 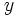$y\,$ such that 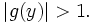$|g(y)| >1.\,$ Recall that 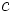$c\,$ cannot be zero.

$\square$

Retrieved from "http://www.efnet-math.org/w/Solutions_for_Dec._30%2C_2006"