Solutions for Jan. 9, 2006 (b)

b) Using Pappus's second theorem (http://mathworld.wolfram.com/PappussCentroidTheorem.html), this could be easy. The shape of this region is a triangle. Using the formula for the centroid of the triangle, we can find the centroid. Then, finding the distance from the centroid to the line y = 3x shouldn't be bad. Using that, we can finally find the area of the triangle, and using the distance of the centroid to the line y = 3x as the radius for Pappus's theorem, we get 2 * π * r * area_of_triangle.

The formula for the centroid(x0,y0) of a triangle (http://en.wikipedia.org/wiki/Centroid) is (x0,y0) = ((1 / 3)(x1 + x2 + x3),(1 / 3)(y1 + y2 + y3)), where (x1,y1), (x3,y3), and (x3,y3) are the vertices of the triangle.

The vertices are (0,0),(4,0) and (4,4) [Draw the region if you have to.] The centroid is (x0,y0) = (8 / 3,4 / 3).

You can derive the formula for point-line distance easily, using vectors and projections in the following manner. Draw a vector from the given point to an arbitrary point on the line. Then, project this vector along the direction vector of the line. Then, find the difference of the two vectors and the magnitude of the resultant vector is the distance between the point and the line.

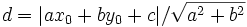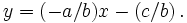
Thus d = |ax_0 + by_0 +c| / \sqrt{a^2+b^2} where y = (-a/b)x -(c/b)\,.

We have a = − 3, b = 1, and c = 0. (x0,y0) is the point, which in our case is the centroid, so (x0,y0) = (8/3,4/3).

This gives 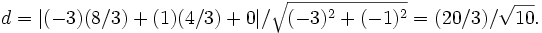d = |(-3)(8/3) + (1)(4/3) + 0 | / \sqrt{(-3)^2+(-1)^2} = (20/3)/\sqrt{10}.

Now d * 2π * area_of_triangle = volume_of_solid_of_revolution.

The triangle has height = 4, base = 4, so area = .5 * base * height = .5 * 4 * 4 = 8.

The volume of the solid of revolution is 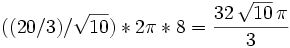((20/3)/\sqrt{10}) * 2\pi * 8 = {{32\,\sqrt{10}\,\pi}\over{3}}.

Retrieved from "http://www.efnet-math.org/w/Solutions_for_Jan._9%2C_2006_%28b%29"