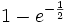Solutions for Jan. 9, 2006 (c)

Solution by i_c-Y

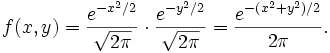
Since X and Y are independent random variables, the joint density function is the product of their density functions, which is $f(x,y)=\frac{e^{-x^2/2}}{\sqrt{2\pi}} \cdot \frac{e^{-y^2/2}}{\sqrt{2\pi}}=\frac{e^{-(x^2+y^2)/2}}{2\pi}.$

Note that the region $x 2 + y 2 < 1$ is a circle centered at the origin with radius 1. Thus, if we convert this region into polar coordinates, $dA=r\,drd\theta$ .

The region can be written as $θ$ goes from $0$ to $2π$ , and $r$ goes from 0 to 1 and we integrate the joint probability density function over that region. The integrand can be rewritten using $x 2 + y 2 = r 2$ as 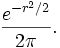$\frac{e^{-r^2/2}}{2\pi}.$ So now you have 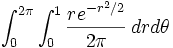$\int_0^{2\pi}\int_0^1 \frac{re^{-r^2/2}}{2\pi}\,drd\theta$ which is an easy double integral to do; use an $u$ -substitution of 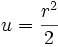$u = \frac{r^2}{2}$ on the inner integral to evaluate it.

This integral evaluates to $1-e^{-\frac12}$

Retrieved from "http://www.efnet-math.org/w/Solutions_for_Jan._9%2C_2006_%28c%29"