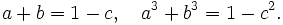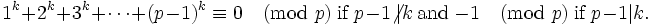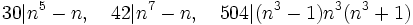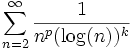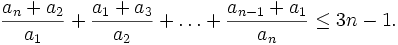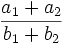POTD 2005-09

Table of contents

1 Friday, Sept. 30, 2005

2 Thursday, Sept. 29, 2005

3 Tuesday, Sept. 27, 2005

4 Monday, Sept. 26, 2005

5 Sunday, Sept. 25, 2005

6 Saturday, Sept. 24, 2005

7 Friday, Sept 23, 2005

8 Wednesday, Sept 14, 2005

9 Tuesday, Sept 13, 2005

10 Thursday, 8 Sep, 2005

11 Monday, 5 Sep, 2005

12 Friday, 1 Sep, 2005

Friday, Sept. 30, 2005

Problem from Chandra

This problem is not technical. Ingenuity is enough. Find all integer solutions to:

$a + b = 1 - c, \quad a^3 + b^3 = 1 - c^2.$

Thursday, Sept. 29, 2005

This problem is not difficult but you may need half a number theory course or maybe some abstract algebra. For integer $k$ and prime $p$ prove that

$1^k + 2^k + 3^k + \dots + (p-1)^k \equiv 0 \pmod{p}\ \mathrm{if}\ p-1 \not | k \ \mathrm{and}\ -1\pmod{p} \ \mathrm{if}\ p-1 | k.$

Tuesday, Sept. 27, 2005

Easy problem from Chandra

Prove $n 5 + n 4 + 1$ is never a prime for $n > 1.$

Puzzle (http://www.math.ku.dk/~m05to/opgave.pdf) from Zabrien.

Monday, Sept. 26, 2005

Rerun problems. Very easy. Show:

$30|n^5-n,\quad 42|n^7-n,\quad 504|(n^3-1)n^3(n^3+1)$

Sunday, Sept. 25, 2005

Problem from Chandra

This was a contest problem and might be hard. $p > 3$ is a prime. Find all integers $a, b,$ such that:

a 2 + 3 a b + 2 p (a + b) + p 2 = 0

Saturday, Sept. 24, 2005

Problem by landen. $0 < p < 1$ is real. Show that the following series diverges.

$\sum^\infty_{n=2} \frac{1}{n^p (\log(n))^k}$

Friday, Sept 23, 2005

Rated easy. Find all integral solutions of the equation

a 2 + b 2 + c 2 = a 2 b 2

Wednesday, Sept 14, 2005

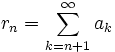Let $\sum^\infty_{n=1} a_n$ be a convergent series of positive terms $a n$ . Let $r_n = \sum^\infty_{k=n+1} a_k$ .

Show that

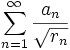$\sum^\infty_{n=1} \frac{a_n}{\sqrt{r_n}}$ converges, and

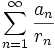$\sum^\infty_{n=1} \frac{a_n}{r_n}$ diverges.

Tuesday, Sept 13, 2005

From Polytope via Kit.

$Y n$ iid random variables uniform on $[0,1]$ . $X$ is the smallest $n$ such that 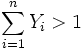$\sum^n_{i=1} Y_i > 1$ . Show that $E (X) = e$ .

Thursday, 8 Sep, 2005

(Circular arrangement of numbers) Suppose positive integers 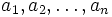$a_1,a_2,\dots,a_n$ satisfy

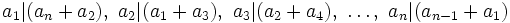$a_1|(a_n+a_2),\ a_2|(a_1+a_3),\ a_3|(a_2+a_4),\ \dots,\ a_n|(a_{n-1}+a_1)$ .

Think of the $a i$ 's as placed in a circular arrangement; then each number divides the sum of its two neighbors. Prove that

$\frac{a_n+a_2}{a_1} + \frac{a_1+a_3}{a_2} + \dots + \frac{a_{n-1}+a_1}{a_n}\le 3n-1.$

This is the Problem of the Day section for September 2005.

The problems are shown in reverse order.

Monday, 5 Sep, 2005

From Radcliffe: Let $a 0 = 1$ and $a n = s i n (a n - 1)$ for $n > 0$ . Find 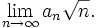$\lim_{n\to\infty} a_n\sqrt{n}.$

Interesting answer, neither 0 or $\infty$ . solution (http://www.efnet-math.org/TopicSolution.pdf)

Show sequence 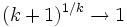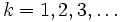$(k+1)^{1/k} \rightarrow 1$ , $k=1,2,3,\dots$ For smart pre-calc or calc I students. No logs or l'Hopital.

Friday, 1 Sep, 2005

1. Greatest common divisor problem for beginning students. Experienced people, please do not solve in the channel. This is for Images, Karlsen, ...

Show there is no cancellation in the fraction

$\frac{a_1+a_2}{b_1+b_2}$

if $a_1b_2 - a_2b_1 = \pm1.$

2. Prove that for $n > 1$ there are no integers $a > b > 1$ such that $(a n - b n) | (a n + b n)$ .

Retrieved from "http://efnet-math.org/w/POTD_2005-09"