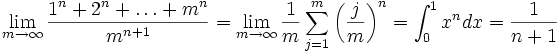Solution July 26, 2007
Solution by landen
Find the following limit in terms of 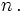
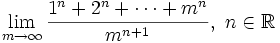 with
with 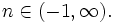
The plan is to use a Riemann sum (http://en.wikipedia.org/wiki/Riemann_integral) to convert the limit into an integral.
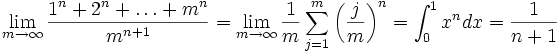
Solution by landen
Find the following limit in terms of 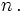
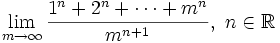 with
with 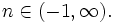
The plan is to use a Riemann sum (http://en.wikipedia.org/wiki/Riemann_integral) to convert the limit into an integral.