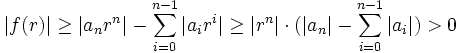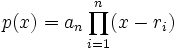Solution June 22, 2007
Problem
Does there exist a a sequence  in
in  , such that for each
, such that for each  , and for each n, the polynomial
, and for each n, the polynomial 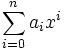 is irreducible in
is irreducible in ![\mathbb Z[x]](https://efnet-math.org/wiki/images/math/3182ba9f80992f4f3bf853027b5dc2a3.png) ?
?
Solution
Yes.
Lemma: Let 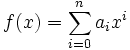 with
with 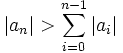 . Then, any complex root of f(x) has absolute value less than 1.
. Then, any complex root of f(x) has absolute value less than 1.
Proof: Assume 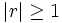 . Then, by the triangle inequality,
. Then, by the triangle inequality,
so 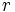 is not a root of
is not a root of 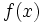 . The Lemma follows.
. The Lemma follows. 
Now define 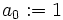 and
and  where
where 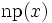 denotes the smallest prime number larger than
denotes the smallest prime number larger than  . This sequence satisfies the conditions of the problem.
. This sequence satisfies the conditions of the problem.
Proof: Assume there is a n such that 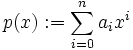 is reducible, i.e.
is reducible, i.e.
with non-constant polynomials 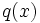 and
and 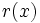 .
Because the leading coefficient of
.
Because the leading coefficient of 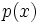 is prime, one of the polynomials
is prime, one of the polynomials 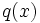 and
and 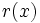 must be monic (have leading coefficient
must be monic (have leading coefficient 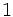 ). Assume without loss of generality that
). Assume without loss of generality that 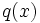 is monic.
is monic.
By the Fundamentel Theorem of Algebra (http://en.wikipedia.org/wiki/Fundamental_theorem_of_algebra) we can write
where 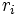 are the complex roots of
are the complex roots of 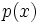 . By our lemma,
. By our lemma, 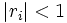 for all
for all 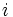 .
.
All roots of 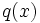 are also roots of
are also roots of 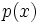 . The constant term of
. The constant term of 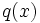 is the product of these roots. The absolute value of that product is less than
is the product of these roots. The absolute value of that product is less than 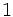 , so the constant term of
, so the constant term of 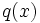 - being an integer - must be
- being an integer - must be 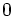 . But then
. But then
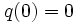 , a contradidiction because 0 is not a root of
, a contradidiction because 0 is not a root of 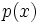 - indeed,
- indeed, 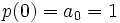 .
.
So 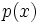 must be irreducible as claimed.
must be irreducible as claimed.