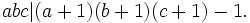Solution May 25, 2007
Problem
Given natural numbers 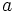 ,
, 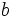 and
and 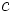 that are pairwise distinct and satisfy
that are pairwise distinct and satisfy
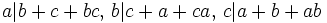 ,
,
prove that at least one of the numbers 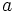 ,
, 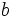 ,
, 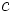 is not prime.
is not prime.
Solution
Assume that a,b,c are distinct primes. Further assume without loss of generality that a < b < c.
Note that 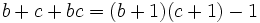 , so
, so 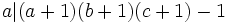 and similar for
and similar for 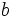 and
and 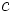 . Also,
. Also, 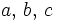 are pairwise coprime, so we have
are pairwise coprime, so we have
Let
-
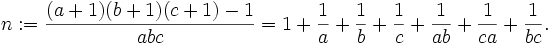 .
.
 is an integer. Obviously,
is an integer. Obviously, 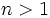 . The right side is a strictly decreasing function in all three variables. Let's check a few cases:
. The right side is a strictly decreasing function in all three variables. Let's check a few cases:
- if
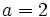 and
and 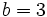 , the right side becomes
, the right side becomes 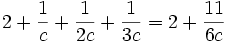 which is never an integer for any
which is never an integer for any 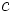
- if
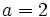 ,
, 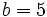 , the right side is not an integer for
, the right side is not an integer for 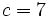 and less than
and less than 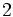 for
for 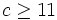 , so it's not an integer then either.
, so it's not an integer then either.
- if
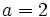 ,
, 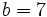 then
then 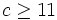 and again,
and again,  .
.
- if
 , then
, then 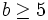 and
and 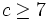 and, (surprise!)
and, (surprise!)  .
.
This shows that  can never be an integer, in contradiction with our assumptions, completing the proof.
can never be an integer, in contradiction with our assumptions, completing the proof.