Solution May 30, 2007

Problem

Let a,b,c,d be positive reals such that $a + b + c + d = 1$ .

Prove that: 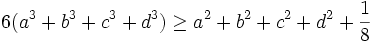$6(a^{3}+b^{3}+c^{3}+d^{3})\geq a^{2}+b^{2}+c^{2}+d^{2}+\frac{1}{8}$ .

Solution

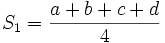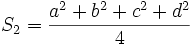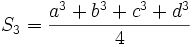Let $S_1=\frac{a+b+c+d}4$ , $S_2=\frac{a^2+b^2+c^2+d^2}4$ and $S_3=\frac{a^3+b^3+c^3+d^3}4$ . By the power mean inequality (http://planetmath.org/encyclopedia/GeneralMeansInequality.html), we have

$S_1 \leq \sqrt{S_2} \leq \sqrt[3]{S_3}$ .

This implies

$24 S_3 \geq 16 S_2 S_1 + 8 S_1^3$

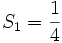Using $S_1 = \frac 14$ , this is equivalent to

$6(a^{3}+b^{3}+c^{3}+d^{3})\geq a^{2}+b^{2}+c^{2}+d^{2}+\frac{1}{8}$

q.e.d.

Retrieved from "https://www.efnet-math.org:443/w/Solution_May_30%2C_2007"