Solution May 30, 2009

Sketch of Proof.

It's easy to see that 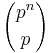${p^n \choose p}$ is divisible by $p n - 1$ . Then,

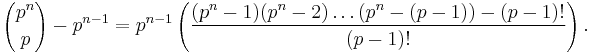
${p^n \choose p} - p^{n-1} = p^{n-1} \left( \frac{(p^n - 1)(p^n - 2)\ldots(p^n - (p-1)) - (p-1)!}{(p-1)!} \right).$

Modulo $p$ , it's clear that the right hand side is divisible by $p$ .

For the variation when $p$ is an odd prime, it suffices to check that $p n + 1$ divides 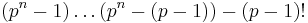$(p^n - 1)\ldots(p^n - (p-1)) - (p-1)!$ .

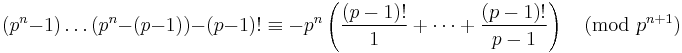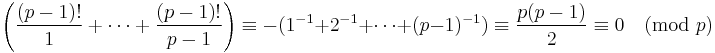$(p^n - 1)\ldots(p^n - (p-1)) - (p-1)! \equiv -p^n \left( \frac{(p-1)!}{1} + \cdots + \frac{(p-1)!}{p-1} \right) \pmod{p^{n+1}}$ . But $\left( \frac{(p-1)!}{1} + \cdots + \frac{(p-1)!}{p-1} \right) \equiv -(1^{-1} + 2^{-1} + \cdots + (p-1)^{-1}) \equiv \frac{p(p-1)}{2} \equiv 0 \pmod{p}$ by wilson's theorem + the fact that every element has unique inverse.

Retrieved from "https://www.efnet-math.org:443/w/Solution_May_30%2C_2009"