Solution Feb 12, 2012

Problem

Suppose $X$ is a finite set such that $| X | = 2 k$ for some positive integer $k$ . Suppose there's a family $F$ of subsets of $X$ , where each element of $F$ has cardinality $k$ , and such that every subset of $X$ having cardinality $k - 1$ is uniquely contained in some element of $F$ . Prove that $k + 1$ is prime.

Solution

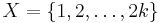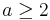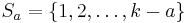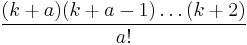Without loss of generality let $X = \{1,2,\ldots, 2k \}$ . For $a \geq 2$ , I claim that the number of sets in $F$ containing $S_a = \{1,2,\ldots, k-a\}$ is precisely $\frac{(k+a)(k+a-1)\ldots(k+2)}{a!}$ .

There are $2 k - (k - a) = k + a$ numbers in $X - S a$ . Choosing any $a - 1$ numbers in $X - S a$ and including them in $S a$ will provide us with a subset of cardinality $k - 1$ , which, by the condition on $F$ , is uniquely contained in some set in $F$ . There are clearly $a!$ repetitions in creating a set in this manner, so the claim is proved.

Since 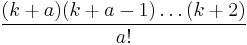$\frac{(k+a)(k+a-1)\ldots(k+2)}{a!}$ is integer for all 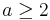$a \geq 2$ , it's now easy to see that $k + 1$ is prime.

Retrieved from "https://www.efnet-math.org:443/w/Solution_Feb_12%2C_2012"