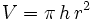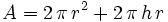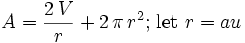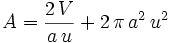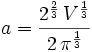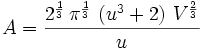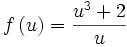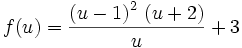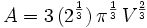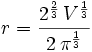Design a Tin Can (harder pre-cal but easy calc)

Design a tin can so that the total area including a top and bottom is minimized for a required volume. The can has radius $r$ and height $h$ .

$V=\pi\,h\,r^2$

$A=2\,\pi\,r^2+2\,\pi\,h\,r$

$A={{2\,V}\over{r}}+2\,\pi\,r^2\mbox{; let } r=au$

$A={{2\,V}\over{a\,u}}+2\,\pi\,a^2\,u^2$

The reason for changing variables was to choose a nice $a$ which will make $u$ unitless and make the problem generic since the numerical value of $V$ has nothing to do with the essence of the problem. Also, we can get rid of the $π$ so that the function to minimize is easy to study. The value of $a$ landen picked is not as arbitrary as it looks at first and there was some experimentation with the substitution using Maxima (http://maxima.sourceforge.net) to find a good one.

$a={{2^{{{2}\over{3}}}\,V^{{{1}\over{3}}}}\over{2\,\pi^{{{1}\over{3 }}}}}$

$A={{2^{{{1}\over{3}}}\,\pi^{{{1}\over{3}}}\,\left(u^3+2\right)\,V^{ {{2}\over{3}}}}\over{u}}$

Now all we need to do is minimize:

$f\left(u\right)={{u^3+2}\over{u}}$

A little playing around with a calculator suggest that the minimum value is $f (u) = 3$ and that this happens when $u = 1$ . So we rewrite f(u) to emphasize 3 and 1 and we hit the jackpot.

$f(u)={{\left(u-1\right)^2\,\left(u+2\right)}\over{u}}+3$

In this form it is obvious that the minimum value of $f (u) = 3$ and this happens when $u = 1$ .

$A=3\,(2^{{{1}\over{3}}})\,\pi^{{{1}\over{3}}}\,V^{{{2}\over{3}}}$

$r={{2^{{{2}\over{3}}}\,V^{{{1}\over{3}}}}\over{2\,\pi^{{{1}\over{3 }}}}}$

$h={{2^{{{2}\over{3}}}\,V^{{{1}\over{3}}}}\over{\pi^{{{1}\over{3}}} }}=2r$

Retrieved from "http://efnet-math.org/w/Design_a_Tin_Can_%28harder_pre-cal_but_easy_calc%29"