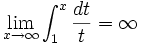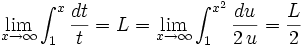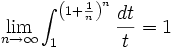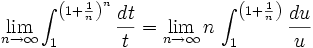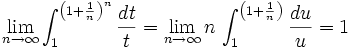Famous Limit
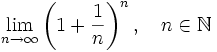 is a famous limit that is in all Calc I books. Here are some proofs about it that are usually done other ways.
is a famous limit that is in all Calc I books. Here are some proofs about it that are usually done other ways.
Theorem IA
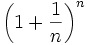 is increasing
is increasing
Proof:
A method Polytope saw someplace.
Consider the 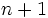 numbers
numbers ![\left[1,\ 1+\frac{1}{n},\ 1+\frac{1}{n},\ \cdots ,\ 1+\frac{1}{n}\right]](https://efnet-math.org/wiki/images/math/bc0ac293d89b865f878408cd9869a367.png)
These have a geometric mean. 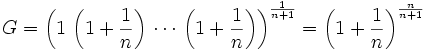
These have an arithmetic mean.
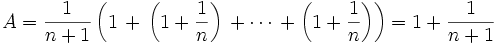
Now we use the Arithmetic Mean-Geometric Mean Inequality (http://en.wikipedia.org/wiki/Inequality_of_arithmetic_and_geometric_means).
 and
and 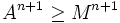
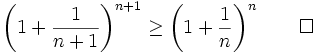
Theorem IB
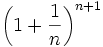 is decreasing.
is decreasing.
The proof of IA can be adapted to prove IB.
Consider the 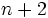 numbers
numbers ![\left[1,\ 1+\frac{1}{n},\ 1+\frac{1}{n},\ \cdots ,\ 1+\frac{1}{n}\right]](https://efnet-math.org/wiki/images/math/bc0ac293d89b865f878408cd9869a367.png)
These have a geometric mean. 
Next we can compare 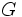 to the harmonic mean,
to the harmonic mean, 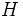 , using the Geometric Mean - Harmonic mean inequality. (http://planetmath.org/encyclopedia/ArithmeticGeometricMeansInequality.html)
, using the Geometric Mean - Harmonic mean inequality. (http://planetmath.org/encyclopedia/ArithmeticGeometricMeansInequality.html)
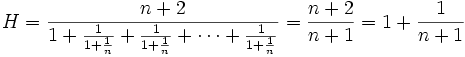



Theorem IC
The sequences from IA and IB both converge to the same limit.
Proof
Since the sequence of IB is decreasing and positive it is bounded below by 0. The sequence of IB converges due to Proposition 3.1.9 at this site. (http://pirate.shu.edu/~wachsmut/ira/numseq/sequence.html)
For all n, 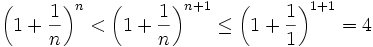
So the convergence of the sequence from IA follows by the same proposition.
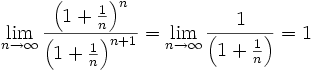
So both sequences have the same limit.

Lemma IIL
Proof
As  increases, the integral smoothly and monotonically increases beause its first derivative is
increases, the integral smoothly and monotonically increases beause its first derivative is  . Suppose it reaches a finite limit
. Suppose it reaches a finite limit 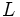 . Use the substitution
. Use the substitution 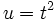 .
.
Since 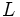 cannot be
cannot be 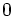 ,
, 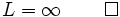
Theorem II
Let 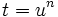
Since 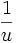 is monotonically decreasing, it maximum occurs at 1 and its minimum occurs at
is monotonically decreasing, it maximum occurs at 1 and its minimum occurs at 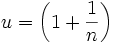 . We can use these and the difference of the limits,
. We can use these and the difference of the limits, 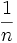 , to bound the integral.
, to bound the integral.
Using the squeeze theorem (http://en.wikipedia.org/wiki/Squeeze_theorem). Then from the Lemma IIL 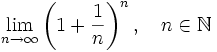 is finite since the limit of the integral is infinite for an infinite upper limit.
is finite since the limit of the integral is infinite for an infinite upper limit.