Farmer Optimizes Fence (hard pre-cal but easy calc)
A classic problem is about the farmer who wants to decide the proportions of a field which is perhaps next to a river and which is to be fenced and subdivided. The goal is to minimize the length of fence P necessary for a given area A of field and a given method of subdividing by internal fences across the area. In the illustration there are 3 runs of fence of length L parallel to the river and 5 runs of fence of width W perpendicular to the river and there is no fence along the river. It is just as easy to generalize to M runs of fence parallel to the river and N runs of fence perpendicular to the river. Whether there is fence along the bank of the river and whether the parallel subdividing fences are equally spaced is just a decoration. Two equations describe the situation.
If this general case seems too hard skip to the special case at then end with just a simple fence around the field but not along the river.
Solution I
L and W have the units of length and A has the units of length squared. It is a matter of experience that it helps to use compatible units for comparing. In this case we can minimize P2 instead of P, since it has the units of length squared and will compare easily to the area (maybe).
There is a fairly well known identity which we can apply and see what happens. It is important to try ideas even if you cannot see they lead anywhere:
using
To minimize P2 we can't adjust 4MNA which is a constant. The next term is never negative so it only makes P2 larger, 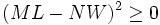 .
.
The minimum P occurs when ML = NW or the total fence along the river is equal in length to the total fence parallel to the river. Polytope pointed out that sometimes the cost of fence along the river is different to the cost of fence parallel to the river. M and N can be changed to reflect the number of runs times the cost and the answer is that the total costs in the two directions are the same.
Solution II
Starting with the original equations we can eliminate L from the first one by using the second:
We have a quadratic equation in W and we can complete the square as an experiment to see if it helps. This is not done to solve for W but just to put the equation in a different form which may lead somewhere. Multiply by 4N first to avoid fractions.
Once again the right hand side has a minimum when a squared quantity is 0.
It is important to note that completing the square removed the term that was linear in W and this allowed a simple interpretation. In the equation:
It is the PW term which prevents a simple interpretation.
Special Case
In the special case there are no cross fences subdividing the field. The river is one boundary of the field. There are two fences of length W perpedicular to the river. A single fence of length L parallel to the river marks the fourth side of the field. If we remove the river and put an idential field where it is we get a fully fenced field of length L and width 2W. If we know that a square has the most area for a given perimeter then we know W = L / 2 for the best design. So all we have to do is show that a square is the best design for a fully fenced field.
Suppose we have full fenced rectangles of perimeter P = 2L + 2W. We can arrange 4 of them inside a square with side P / 2. If our rectangles are squares then 4 of them obviously fill the bigger square of side P / 2, so we can't do better than to use squares. In the following figure we see that 4 oblong rectangles cannot cover the square of side P / 2 but leave an unfilled region of side L − W in the center. If L = W then this vacant space is filled. So a square is best.
%20-%20EFnetMath_files/Farm2.png)
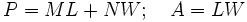


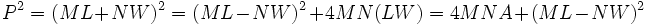
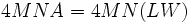


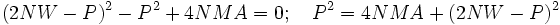
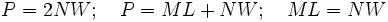
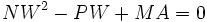
%20-%20EFnetMath_files/Squares2.png)