From a Point to a Plane, distance, etc

The usual form of the 3-d equation of a general plane is:

$ax + by + cz = d\mbox{ with }\mathbf{v}=[a,b,c]\mbox{ a vector normal to the plane}\,$

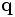Suppose we have an external point $\mathbf{p}=[x_1,y_1,z_1]$ and wish to know the shortest distance to the plane and where on the plane the closest approach point, $\mathbf{q}$ , is. The shortest distance line to the plane is perpendicular to the plane. To see this draw some other line, 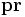$\mathbf{pr}$ , to a point, 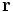$\mathbf{r}$ , on the plane and make the right triangle 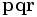$\mathbf{pqr}$ . 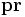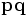The distance along the line $\mathbf{pr}$ is the hypotenuse of the right triangle and is therefore longer than $\mathbf{pq}$ .

A convenient method to find the point 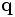$\mathbf{q}$ on the plane at the foot of the perpendicular is to write the equation of a line through 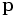$\mathbf{p}$ which is parallel to 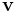$\mathbf{v}$ , the normal to the plane. Using a simple scalar variable 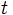$t\,$ as a parameter for the line and solving for the intersection with the plane, we have:

$[x,y,z] = [x_1,y_1,z_1] + t[a,b,c]\,\mbox{ parametric equation of the line}$

$inserting the parameterized [x, y, z] into the equation for the plane:$

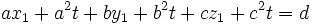
$ax_1 + a^2t + by_1 + b^2t + cz_1 +c^2t = d\,$

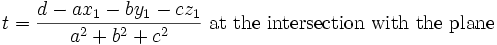
$t= \frac{d-ax_1-by_1-cz_1}{a^2 + b^2 + c^2}\mbox{ at the intersection with the plane}$

This formulation is good for a computer program and it is good to check that the denominator is not zero. If the denominator is zero the plane was no good to begin with.

$\mathbf{q} = [x_1,y_1,z_1] + t[a,b,c] = [x_1,y_1,z_1] + \left(\frac{d-ax_1-by_1-cz_1}{a^2 + b^2 + c^2}\right)[a,b,c]$

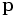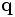We can use the distance formula (http://en.wikipedia.org/wiki/Distance#The_distance_formula) to find the distance from $\mathbf{p}$ to $\mathbf{q}$ :

$\left|\mathbf{q}-\mathbf{p}\right|=\left|\frac{d-ax_1-by_1-cz_1}{a^2 + b^2 + c^2}\right|\left|[a,b,c]\right|\ =\ \left|\frac{d-ax_1-by_1-cz_1}{\sqrt{a^2 + b^2 + c^2}}\right|$

Retrieved from "http://efnet-math.org/w/From_a_Point_to_a_Plane%2C_distance%2C_etc"