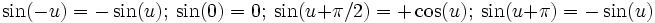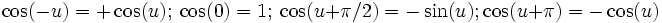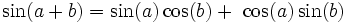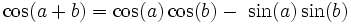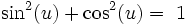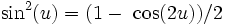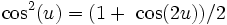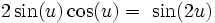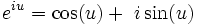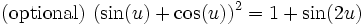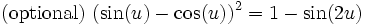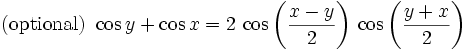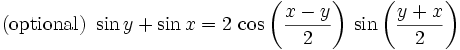Math Trig Identities

There are several trig identities which are necessary for calculus. They are not hard to derive but you may not have time to derive them on a test. Also, you need to be so fluent in using them that you can introduce them to solve problems which don't have trig functions in them to start with. Maybe the best thing to do is just memorize them.

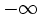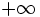Another thing to memorize is the general appearance of the graphs of sin,cos, and tan from − 2π to 2π. Be sure you understand sin and cos as periodic functions with period 2π which stretch from -\infty to +\infty along the whole line of real numbers. Sine and Cosine are bounded. The tangent function is not bounded. Treating them just as ratios in right triangles is too limiting for college math, engineering, and the sciences.

Here is a suggested set of identities to memorize:

  1. \sin(-u) = -\sin(u);\ \sin(0) = 0;\ \sin(u + \pi/2) = +\cos(u);\ \sin(u + \pi) = -\sin(u)
  2. \cos(-u) = +\cos(u);\ \cos(0) = 1;\ \cos(u + \pi/2) = -\sin(u); \cos(u + \pi) = -\cos(u)
  3. \sin(a + b) = \sin(a)\cos(b) +\ \cos(a)\sin(b)
  4. \cos(a + b) = \cos(a)\cos(b) -\ \sin(a)\sin(b)
  5. \sin^2(u) + \cos^2(u) =\ 1
  6. \sin^2(u) = (1 -\ \cos(2u))/2
  7. \cos^2(u) = (1 +\ \cos(2u))/2
  8. 2\sin(u)\cos(u) =\ \sin(2u)
  9. e^{iu} = \cos(u) +\ i\sin(u)
  10. \mathrm{(optional)\ }\tan(a + b) = \frac{\tan(a) + \tan(b)}{1 - \tan(a)\tan(b)}
  11. \mathrm{(optional)\ }(\sin(u)+\cos(u))^2 = 1 + \sin(2u)\,
  12. \mathrm{(optional)\ }(\sin(u)-\cos(u))^2 = 1 - \sin(2u)\,
  13. \mathrm{(optional)\ }\cos y+\cos x=2\,\cos \left({{x-y}\over{2}}\right)\,\cos \left({{y+ x}\over{2}}\right)
  14. \mathrm{(optional)\ }\sin y+\sin x=2\,\cos \left({{x-y}\over{2}}\right)\,\sin \left({{y+ x}\over{2}}\right)

The symmetries between sin and cos with a few sign changes here or there make learning the identities easy but can be confusing, especially when under pressure. A 95% memorization of the list can be extended to a 100% recall by quick comparisons.

Suppose you almost remember #5. Is #5: sin2(u) = (1 − cos(2u)) / 2 or is it sin2(u) = (1 + cos(2u)) / 2? The first one is the correct identity. If you can't remember the sign on a quiz then recall sin(0) = 0 and cos(0) = 1. If you put 0 in for u you can determine the missing sign.

The variables u, a, b, etc., in the identities can be ANY real expressions including constants. They do not have to be simple variables. Here are some ideas for how to remember and use identities that are quick enough for use on a test.

Is #3 sin(a + b) = sin(a)cos(b) + cos(a)sin(b) or is it: sin(a + b) = sin(a)cos(b) − cos(a)sin(b) or sin(a + b) = cos(a)cos(b) − sin(a)sin(b) or... etc. The first identity is correct. Try letting a = 0, b=0, a=b, and a=-b and the correct identity will stand out.

No. 6 sin^2(u) = (1 - cos(2u))/2 This has many uses. It also means sin^2(x/2) = (1 - cos(x))/2 and sin^2(3 pi a) = (1 - cos(6 pi a))/2

No. 5 sin^2(u) + cos^2(u) = 1 Divide this by sin^2(u) or cos^2(u) to get 1 + cot^2(u) = csc^2(u) tan^2(u) + 1 = sec^2(u)

When doing an integral you sometimes want to introduce trig into an expression which doesn't have any trig in at first. This is when you need to know the identities backwards and forwards and rearranged, and what those graphs look like. Consider: sqrt(4 - 9x^2) dx x^2 has to be <= 4/9 to keep the sqrt real. x is bounded. So we try x="(2/3)sin(t)" as a substition to simplify this for integration. We had to foresee that sin^2(u) + cos^(u) = 1 could be recast as 4 - 4sin^2(u) = 4cos^2(u)

Next consider: sqrt(4x^2 - 9) dx Now the expression inside the radical is never negative for |x| >= 3/2. When x can go off toward inf we need to use one of the tan or cot identities to get a function that is unbounded. 1 + cot^2(u) = csc^2(u) Recast this as 9csc^2(u) - 9 = 9cot^2(u) Then let x = 3csc(u)/2 to turn the expression in the radical into a perfect square. sqrt(4x^2 - 9) = sqrt((4*9/4)csc^2(u) -9) = 3cot(u) This integral could be done with hyperbolic trig functions, if you have had them.

Identity #9. e^(iu) = cos(u) + isin(u) This identity is the one to know if you are good at deriving and really bad at memorizing. It is not just for complex numbers. Notice: e^(iu)e^(-iu) = e^(i0) = 1 = cos^2(u) + sin^2(u) b00m! Also notice: (e^(iu))^3 = e^(i3u) = cos(3u) + isin(3u) = cos^3(u) + 3icos^2(u)sin(u) + 3i^2cos(u)sin^2(u) + i^3sin^3(u) = cos^3(u) - 3cos(u)sin^2(u) + i(3cos^2(u)sin(u) - sin^3(u)) Since the real and imaginary parts are equal separately we can get: cos(3u) = cos^3(u)-3cos(u)sin^2(u) = 4cos^3(u) - 3cos(u) sin(3u) = 3cos^2(u)sin(u) - sin^3(u) = -4sin^3(u) + 3sin(u)

Identity #10. This is not used as often and most people do not have it memorized. You can derive it on a test about as fast as you can check it:

  1. 2. sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
  2. 3. cos(a + b) = cos(a)cos(b) - sin(a)sin(b)

Just divide these and simlify the right hand side if needed. tan(a+b) = (sin(a)cos(b) + cos(a)sin(b))/(cos(a)cos(b) - sin(a)sin(b) = (tan(a) + tan(b))/(1 - tan(a)tan(b))

Retrieved from "http://efnet-math.org/w/Math_Trig_Identities"