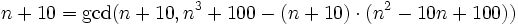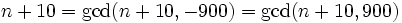Solution July 21, 2007

Problem

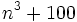What is the largest positive integer $n\,$ such that $n^3+100\,$ is divisible by $n+10\,$ ?

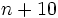Solution

$n + 10 | n 3 + 100$ is equivalent to $gcd(n + 10, n 3 + 100) = n + 10$ By the rules for the $gcd$ (http://en.wikipedia.org/wiki/Greatest_common_divisor) we have

$n+10 = \gcd(n+10, n^3+100)\,$

$n+10 = \gcd(n+10, n^3+100 - (n+10)\cdot(n^2-10n+100))$

$n+10 = \gcd(n+10, -900) = \gcd(n+10, 900)\,$

In other words, $n + 10 | 900$ and the largest such $n$ is $n = 890$ .

Retrieved from "http://efnet-math.org/w/Solution_July_21%2C_2007"