POTD 2005-10

This is the Problem of the Day section for October 2005.

The problems are shown in reverse order.

Table of contents

1 Thursday, Oct. 27, 2005

2 Monday, Oct. 24, 2005

3 Thursday, Oct. 20, 2005

4 Tuesday, Oct. 18, 2005

5 Thursday, Oct. 13, 2005

6 Friday, Oct. 7, 2005

7 Wednesday, Oct. 5, 2005

8 Monday, Oct. 3, 2005

9 Saturday, Oct. 1, 2005

Thursday, Oct. 27, 2005

from Chandra

Find all natural numbers $n$ such that $n 2$ does not divide $n!$ .

Monday, Oct. 24, 2005

from Chandra

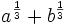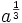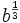$a$ and $b$ are positive rationals such that $a^{\frac{1}{3}} + b^{\frac{1}{3}}$ is also rational. Show that $a^{\frac{1}{3}}$ and $b^{\frac{1}{3}}$ are rational. solution (http://www.efnet-math.org/Sol051024.pdf)

Thursday, Oct. 20, 2005

from dioid

Let $F n$ be the n'th Fibonacci number. Show that:

$d|n \rightarrow F_d | F_n \,$

Tuesday, Oct. 18, 2005

First year number theory level solvers only, please. Show the following has no solutions in integers:

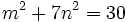
$m^2 + 7n^2 = 30\,$

hint: try mod

Thursday, Oct. 13, 2005

Do the following Op Art sequences have a limit as 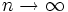$n\rightarrow\infty$ $S_n = \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+ \sqrt{\dots \sqrt{1+\sqrt{1+1}}}}}}}$ radicals nested $n$ deep.

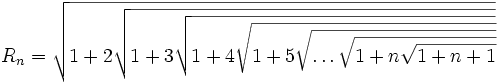
$R_n = \sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+ 5\sqrt{\dots \sqrt{1+n\sqrt{1+n+1}}}}}}}$

If they exist, what are the limits.

solution (http://efnet-math.org/old/RamanujanRadicals.pdf)

Friday, Oct. 7, 2005

From ManchaADD

Given $2 n + 1$ identical books. In how many ways can they be shelved into 3 shelves (top, middle, and bottom) such that the sum of the number of books on any two shelves is greater than the number of books in the remaining shelf?

Wednesday, Oct. 5, 2005

Posed by DavidW2

Given a set S with n elements. What is the probability that any two randomly selected subsets of S (every pair of subsets is equally likely to be chosen) are disjoint? How about two randomly selected non-empty subsets?

Monday, Oct. 3, 2005

From Chandra

Prove that any positive integer not exceeding $n!$ can be written as a sum of at most $n$ distinct factors of $n!.$

Saturday, Oct. 1, 2005

From Chandra

A natural number $k$ has the property that if $k$ divides $n$ , then the number obtained from $n$ by reversing the order of its digits is also divisible by $k$ . Prove that $k$ is a divisor of 99.

Retrieved from "http://efnet-math.org/w/POTD_2005-10"