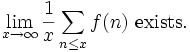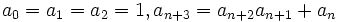POTD 2005-12

You might be able to solve this if you have had experience or a little number theory past a single semester. Here (http://efnet-math.org/math_tech/HyperQuadForm.html) is a solved related problem which shows some ways to attack these problems with elementary theory.

Wednesday, Dec 28, 2005

from nerdy2

Suppose $f : N \to [-1,1]$ is completely multiplicative, show that it has an "average", i.e., show that

$\lim_{x\to \infty} \frac{1}{x} \sum_{n\le x} f(n)\mbox{ exists.}\,$

Tuesday, Dec 27, 2005

from MathKiD

Construct a polynomial of degree 7 with rational coefficients whose Galois group over Q is $S 7$ .

Monday, Dec 26, 2005

from MathKiD (Topics In Algebra by Herstein)

Prove that every finite group having more than two elements has a non-trivial automorphism.

Monday, Dec 19, 2005

Let 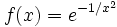$f(x) = e^{-1/x^2}$ for $x$ not equal to 0, $f (0) = 0$ . show that $f$ is infinitely differentiable at 0.

Sunday, Dec 18, 2005

A. from landen who heard it from someone. Rated "may take more than 1st semester number theory". Hint

Show that for prime $p$ , $m 2 - p n 2 = - 1$ can be solved in integers if and only if $p = 2$ or p is of the form $4 k + 1$ .

B. from Karlsen

show that 5 divides one and only one of the sides in a primitive pythagorean triplet

Friday, Dec 16, 2005

from MathKiD

Prove that for a prime p there is another prime q for which $n p - p$ is never divisible by q for any integer value of n.

Monday, Dec 12, 2005

From MathKiD

Solve: $\cos(\cos(\cos(\cos x))) = \sin(\sin(\sin(\sin x)))\,$

Wednesday, Dec 7, 2005

Find a topological space $X$ such that $X$ is homeomorphic to $X 2$ but not to 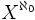$X^{\aleph_0}$ .

Bonus question: Find a compact Hausdorff example.

Sunday, Dec 4, 2005

From MikeJ

What is the maximum length of straight pipe which can be carried around the corner from the 6ft wide hall to the 9ft wide hall?

solution from johanwhee and landen

Saturday, Dec 3, 2005

From MathKiD

Show that given 200 integers you can always choose 100 with sum a multiple of 100.

Extra credit from Polytope Any set of $2 n - 1$ integers has an $n$ -element subset whose sum is divisible by $n$ . solution (http://groups.google.com/group/sci.math/msg/5f209fb0bd89435a?dmode=source)

Friday, Dec 2, 2005

From dioid. This is an International Math Olympiad training problem and was easily solved by Polytope and landen. No advanced number theory needed.

$a_0 = a_1 = a_2 = 1, a_{n+3} = a_{n+2}a_{n+1} + a_n\,$

Show that there for any natural $k$ , exists an $a n$ that is divisible by $k$ .

Thursday, Dec 1, 2005

From landen for crostyna

For $n > 0$ show that:

$\sum_{k=2}^\infty \frac{1}{\sqrt{k}\ln^n(k)} \mbox{ diverges.}\,$

Extra Credit: Do the problem with at least three methods, e.g., like these (http://pirate.shu.edu/projects/reals/numser/tests.html).

Retrieved from "http://efnet-math.org/w/POTD_2005-12"