POTD 2006-01

This is the Problem of the Day section for January 2006.

The problems are shown in reverse order.

Table of contents

1 Sunday, Jan 29, 2006

2 Tuesday, Jan 24, 2006

3 Friday, Jan 20, 2006

4 Wednesday, Jan 18, 2006

5 Tuesday, Jan 17, 2006

6 Friday, Jan 13, 2006

7 Monday, Jan 9, 2006

8 Saturday, Jan 7, 2006

9 January, 5, 2006

Sunday, Jan 29, 2006

From Anil

let $F$ be a subfield of $C$ which contains $i$ , and let $K$ be a Galois extension of $F$ whose group is $C 4$ . Is it true that K has the form $F (α)$ , where 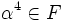$\alpha^4 \in F$ ?

Tuesday, Jan 24, 2006

From Anil

$G$ is an abelian group. a and b are elements of G such that $a m = b n = (a b) k$ where m, n, k, are positive integers no two of which have a common factor. Show that $a = b = 1$ . Is this necessarily true in a non-abelian group?

Friday, Jan 20, 2006

From Anil

How many real solutions does $2 x = 1 + x 2$ have?

Wednesday, Jan 18, 2006

From Anil

Find all solutions to $x n + 1 - (x + 1) n = 2001$ in positive integers $x$ , $n$ .

Ugly solution by landen

Tuesday, Jan 17, 2006

From Anil

Prove that $2 * cos((2 * π) / 7)$ satisfies $x 3 + x 2 - 2 * x - 1 = 0$ . solution

Friday, Jan 13, 2006

From Anil

Prove that the polynomial $f (x) = x 4 + 2 x + 2$ is irreducible over the field of rational numbers.

Monday, Jan 9, 2006

From Anil

Prove that any complex matrix can be brought to triangular form by a unitary matrix.

Saturday, Jan 7, 2006

From Kit

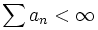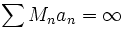Let $M n > 0$ be such that $M_n \to \infty$ . Show there is a sequence $a n > 0$ with $\sum a_n < \infty$ but $\sum M_n a_n = \infty$ .

I used functional analysis to prove it, but my proof was silly (http://mathsscratchpad.blogspot.com/2006/01/silly-proofs-1.html). There's a fairly easy elementary proof.

January, 5, 2006

from Anil

If F is the real field, prove that it is impossible to find matrices 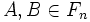$A, B \in F_n$ such that $A B - B A = 1$ .

Retrieved from "http://efnet-math.org/w/POTD_2006-01"