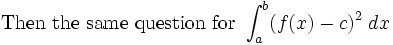POTD 2006-05

Table of contents

1 May 2006

1.1 Saturday, May 27, 2006
1.2 Tuesday, May 16, 2006
1.3 Saturday, May 6, 2006
1.4 Friday, May 5, 2006
1.5 Tuesday, May 2, 2006

May 2006

Saturday, May 27, 2006

from i_c-Y This is a HS problem, uni students please dont give it away before noon UTC, May 28.

Find indefinte integral:

$\int \sqrt{\tan(x)}dx$

Solution here

Tuesday, May 16, 2006

Anil

Show that (5^125 - 1)/(5^25 - 1) is composite.

Saturday, May 6, 2006

landen is celebrating his first birthday which can be written as a sum of squares two distinct ways. Changing the order of the sum is not considered distinct. Find his age. Then write his date of birth as an 8 digit integer $y y y y 0506$ where $y y y y$ is the year. Find an integer solution to: $y y y y 0506 = a 2 + b 2 .$

Friday, May 5, 2006

$\mbox{Suppose }G\mbox{ is a finite group, and }n\mbox{ divides the order of }G,\,$

$\mbox{show that }\sharp\{x \in G : x^n = e\,\}\mbox{ is divisible by }n\,$

Tuesday, May 2, 2006

Problem 3 of the #math calc final

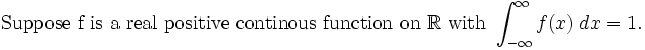
$\mbox{Suppose f is a real positive continous function on }\mathbb{R}\mbox{ with }\int_{-\infty}^\infty f(x)\;dx = 1.$

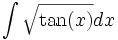
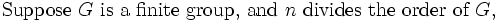
$\mbox{Let }0<\alpha<1,\mbox{ and suppose }[a,b]\mbox{ is an interval of }minimal\mbox{ length such that}\,$

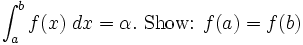
$\int_a^bf(x)\;dx = \alpha.\mbox{ Show: }f(a)=f(b)$

Problem 4 of the #math calc final

$\mbox{Let f be a continuous strictly monotonic function on }[a,b].\,$

$\mbox{Find c so that the integral }\int_a^b |f(x)-c|\; dx\mbox{ is minimized.}$

$\mbox{Then the same question for }\int_a^b (f(x)-c)^2\;dx$

Retrieved from "http://efnet-math.org/w/POTD_2006-05"