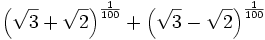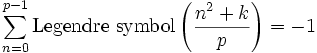POTD 2005-11
This is the Problem of the Day section for November 2005.
The problems are shown in reverse order.
| Table of contents |
Tuesday, Nov 22, 2005
From Anil
Prove that there exists a number divisible by 51000 with no zero digit. Difficulty beginner level. No advanced theorems. solution
Monday, Nov 21, 2005
From Psiko , Show that:
is irrational. solution
Monday, Nov 14, 2005
From Karlsen. Math pros please do not solve this in the channel.
In 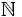 , the positive integers, there is a Pythagorean right triangle with sides x,y,z and an inscribed circle of radius r.
, the positive integers, there is a Pythagorean right triangle with sides x,y,z and an inscribed circle of radius r.
- x2 + y2 = z2 and r = 3, find all possible x,y,z
Hint: There are 3 solutions. Can you prove this? solution
Sunday, Nov 13, 2005
Find indefinite integral:
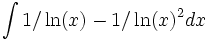
Saturday, Nov 12, 2005
Conjecture of nodar
For p > 2, a prime, and k relatively prime to p,
nerdy2 has solved it and it is fairly easy if you recall your quadratic residue introduction. solution
<nerdy2> note that this suggests another problem: suppose p is a prime, p = 1 mod 4, and k is relatively prime to p, then sum(n=0..p-1) (k - n^2/p) = -1
Friday, Nov 11, 2005
From Dedekind
Find a sequence of functions ![f_n : [0, 1] \to \mathbb{R}](https://efnet-math.org/wiki/images/math/37c6b37ec020abe8de1b9b551ed289c9.png) such that
such that  ,
,  and
and 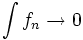 . (the lim sup and inf are pointwise).
. (the lim sup and inf are pointwise).
Tuesday, Nov. 8, 2005
Consider a random walk on the integer positions k=0,1,...,2b, such that given that the position is at k at a time slot the probability to be at position k-1 at next time slot is k/(2b+1), the probability to be at position k next time slot is 1/(2b+1), the probability to be at position k+1 next time slot is (2b-k)/(2b+1). What is the stationary probability distribution (the limiting probability distribution as time tends to infinity) for the positions?
Extra Credit What is the variance of the stationary probability distribution?
Monday, Nov. 7, 2005
Let 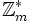 be the residues
be the residues 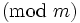 which are relatively prime to
which are relatively prime to  .
.
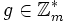 has order
has order  which means that
which means that 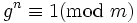 and
and  is the smallest positive integer with this property.
Show that
is the smallest positive integer with this property.
Show that 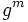 has order
has order 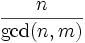 . Where
. Where  is the greatest common divisor function.
is the greatest common divisor function.
Extra Credit
This is a more general version in a group 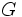 .
.
Let 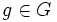 with
with 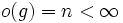 . Then for every integer
. Then for every integer 
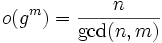
Friday, Nov. 4, 2005
Show that if 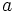 and
and 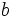 are integers then
are integers then 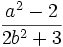 is not.
is not.
landen used Legendre symbols to solve this. There may be a more elementary solution.