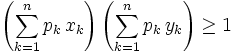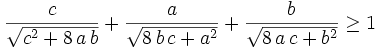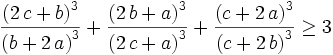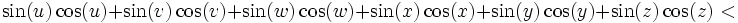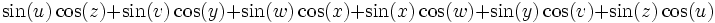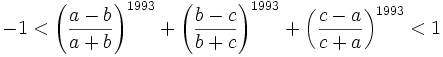POTD 2006-07

Table of contents

1 July 2006

1.1 Sunday, July 30, 2006
1.2 Saturday, July 29, 2006
1.3 Thursday, July 27, 2006
1.4 Monday, July 24, 2006
1.5 Saturday, July 22, 2006
1.6 Friday, July 21, 2006
1.7 Wednesday, July 19, 2006
1.8 Monday, July 17, 2006
1.9 Saturday, July 8, 2006
1.10 Friday, July 7, 2006
1.11 Wednesday, July 5, 2006
1.12 Monday, July 3, 2006
1.13 Sunday, July 2, 2006

July 2006

Sunday, July 30, 2006

from Fermat

Source: IMO 2006

Determine all pairs (x, y) of integers such that

$1 + 2 x + 2 2 x + 1 = y 2$ .

from HiLander

Source: I don't remember, but it's not mine originally.

Rate: Fairly easy.

Suppose you have any $2 n$ points in the plane, no three collinear.

Prove that for each $j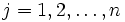$ , $j = 1,2,\ldots,n$ , there is a line where $j$ points lie on one side, $2 n - j$ points lie on the other.

Saturday, July 29, 2006

from landen

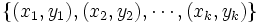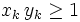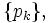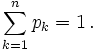A sequence of points $\{(x_1,y_1),(x_2,y_2),\cdots,(x_k,y_k)\}\,$ has the property that all $x_k,\,y_k \,>0$ and all the products $x_k\, y_k\ge 1\,$ . A sequence of positive weights $\{p_k\},\,$ could be probabilities, has the property that $\sum_{k=1}^n p_k =1\, .$ Show that:

$\left( \sum _{k=1}^n p_k\,x_k\right)\left( \sum _{k=1}^n p_k\,y_k\right)\ge 1$

Thursday, July 27, 2006

from Polytope

hard: Show that if an equilateral triangle is dissected into a finite number of smaller equilateral triangles then two of the smaller triangles are congruent.

Monday, July 24, 2006

from HS contest

Show that for all positive reals $a, b, c,$

${{c}\over{\sqrt{c^2+8\,a\,b}}}+{{a}\over{\sqrt{8\,b\,c+a^2}}}+{{b }\over{\sqrt{8\,a\,c+b^2}}}\ge1\,$

Solution by landen

Saturday, July 22, 2006

from Titu Andreescu

Much easier than the July 21, 2006 problem

$\mbox{Show that for all nonzero reals }a,b,c,\,$

$\frac{a^2}{b^2}+ \frac{b^2}{c^2} + \frac{c^2}{a^2} \ge \frac{a}{c} + \frac{c}{b} + \frac{b}{a}$

 Solution

Friday, July 21, 2006

Show that for all positive reals, a,b,c,

${{\left(2\,c+b\right)^3}\over{\left(b+2\,a\right)^3}}+{{\left(2\,b+ a\right)^3}\over{\left(2\,c+a\right)^3}}+{{\left(c+2\,a\right)^3 }\over{\left(c+2\,b\right)^3}}\ge 3$

Solution (http://int-e.home.tlink.de/math/prob0721.pdf) by int-e

Wednesday, July 19, 2006

from landen level is PreCalc IV

Pick six numbers between 0 and $π$ /2 such that $0 < u < v < w < x < y < z < π / 2$ show that:

$\sin(u)\cos(u)+\sin(v)\cos(v)+\sin(w)\cos(w)+\sin(x)\cos(x)+\sin(y)\cos(y)+\sin(z)\cos(z)<\,$

$\sin(u)\cos(z)+\sin(v)\cos(y)+\sin(w)\cos(x)+\sin(x)\cos(w)+\sin(y)\cos(v)+\sin(z)\cos(u)\,$

Monday, July 17, 2006

from landen for zigggy

If $a, b,$ and $c$ are real numbers independently and uniformly distributed in (-1,1), what is the chance the quadratic equation $a x 2 + b x + c$ has two real roots. Try to get an exact answer. It is OK to use logs, sin, cos, $π$ , etc., in the solution. landen got .63 with a crude computer simulation program. The float of the exact answer landen got is 0.6272067094911065535625471212. Karlsen got 0.6273 running the simulation program on a good computer.

Saturday, July 8, 2006

from yannick

Show that for Real $a, b, c > 0$

$-1 < \left(\frac{a-b}{a+b}\right)^{1993}+\left(\frac{b-c}{b+c}\right)^{1993}+\left(\frac{c-a}{c+a}\right)^{1993}<1$

First Solution (http://int-e.home.tlink.de/math/prob0708.pdf) by int-e

Friday, July 7, 2006

from landen

Rate: very easy, for everyone

For $n$ , an integer, what is the biggest value you can get for the greatest common divisor of $15 n + 6$ , and $7 n + 1$

Wednesday, July 5, 2006

from yannick

Rated: very easy, for everyone

Find a set of 2006 positive integers such that the sum of their reciprocals is 1.

Solution from landen

Monday, July 3, 2006

from Polytope

Not hard once you figure out a way to attack it.

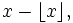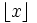Let $x$ be a positive real, $frac(x)$ is the function $x - \lfloor x \rfloor,$ where $\lfloor x \rfloor$ is the floor function (http://en.wikipedia.org/wiki/Floor_function).

Show that $frac(x) = frac(x2) = frac(x3)$ implies x is an integer.

Bonus Show that $frac(x) = frac(x2) = frac(xn)$ where $n$ is an integer greater than 2, implies $x$ is an integer.

Solution from landen.

Sunday, July 2, 2006

Define a sequence of polynomials as follows:

From Kit

$w 0 (x) = 0$

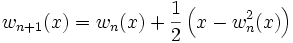
$w_{n+1}(x) = w_n(x) + \frac{1}{2} \left( x - w_n^2(x) \right)$

Show that 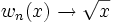$w_n(x) \to \sqrt{x}$ uniformly on $[0,1]$

I streamlined my proof with the use of a biggish theorem, but I suspect there's an elementary proof.

(If you care, I used this as a lemma to produce a nice proof of the Stone Weierstrass theorem)

Retrieved from "http://efnet-math.org/w/POTD_2006-07"