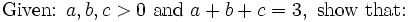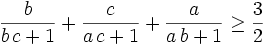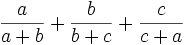POTD 2006-08

Table of contents

1 August 2006

1.1 Monday, 28th of August
1.2 Sunday, 27th of August
1.3 Tuesday, 22nd of August
1.4 Saturday, 19th of August
1.5 Thursday, 18th of August
1.6 Saturday, 12th of August
1.7 Wednesday, 9th August
1.8 Monday, August 7, 2006
1.9 Thursday, August 3, 2006
1.10 Tuesday, August 1, 2006

August 2006

Monday, 28th of August

from Chandra

By Prof. Vasile Cîrtoaje

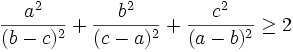
If a, b, c are distinct real numbers, then $\frac{a^{2}}{(b - c)^{2}} + \frac{b^2}{(c - a)^2}+\frac{c^{2}}{(a - b)^2} \geq 2$

Solution by landen.

Sunday, 27th of August

From Kit (in a particularly sadistic mood).

Evaluate 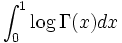$\int_0^1 \log \Gamma(x) dx$ , where $Γ$ is the gamma function (http://en.wikipedia.org/wiki/Gamma_function)

Solution

Tuesday, 22nd of August

Let 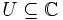$U \subseteq \mathbb{C}$ be a bounded domain and 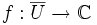$f : \overline{U} \to \mathbb{C}$ a non-constant continuous function which is analytic on $U$ . Show that if $| f (z) | = 1$ on the boundary of $U$ then $f$ takes the value $0$ somewhere in $U$

Saturday, 19th of August

from Kit

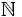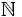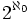Classify all $σ$ -algebras on $\mathbb{N}$ . Use your classification to show that every infinite $σ$ -algebra on $\mathbb{N}$ has cardinality $2^{\aleph_0}$ .

(The answer is nicer than you'd expect.)

Thursday, 18th of August

from Prof. Vasile Cîrtoaje

$\mbox{Given: }a,b,c>0\mbox{ and }a+b+c=3,\mbox{ show that:}\,$

${{b}\over{b\,c+1}}+{{c}\over{a\,c+1}}+{{a}\over{a\,b+1}}\ge\frac{3}{2}$

This was the hardest inequality landen has ever done. Solution

Saturday, 12th of August

from Gillian_S via Kit

Let G be a finite group, 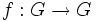$f : G \to G$ a group homomorphism with $f 2 = i d$ and 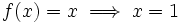$f(x) = x \implies x = 1$ . Show that G is Abelian.

Solution by an infinite number of monkeys.

Wednesday, 9th August

from fiesh via Kit

Show that there is an uncountable subset of 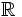$\mathbb{R}$ which contains no uncountable closed sets.

Hint: Any uncountable closed subset of 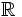$\mathbb{R}$ has cardinality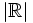 $|\mathbb{R}|$

Warning: Requires moderately advanced knowledge. It's not hard once you spot how to do it, but spotting how to do it might not be easy.

Monday, August 7, 2006

from teknite via Kit

Show that

$\frac{z}{e^z - 1} = 1 - \frac{1}{2} z + \sum\limits_{n=1}^{\infty} \frac{2z^2}{z^2 + 4 n^2 \pi^2}$

from landen This was created by a typo of another expression.

For 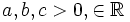$a,b,c >0, \in \mathbb{R}$ find the upper and lower limits of:

$\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}$

Solution by Illustrious Inequality Institute

Thursday, August 3, 2006

from Zabrien

$x y = y x,0 < x < y .$ 1: show (2,4) is the only integer solution. 2: For what values of $x$ does a solution exist. 3: show that an infinite number of rational solutions exist

Solution (http://www.math.ku.dk/~m05to/Aug3solution.pdf) from Zabrien

Tuesday, August 1, 2006

from ermular

One of four different prizes was randomly put into each box of a cereal. If a family decided to buy this cereal until they obtained at least one of each of the four different prizes, what is the expected number of boxes of cereal that must be purchased?

Retrieved from "http://efnet-math.org/w/POTD_2006-08"