POTD 2007-04

Table of contents

1 April 2007

1.1 Thursday, 26th of April
1.2 Tuesday, 17th of April
1.3 Thursday, 12th of April
1.4 Tuesday, 10th of April

April 2007

Thursday, 26th of April

from yannick

Find a polynomial 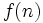$f(n)\,$ which is equivalent to 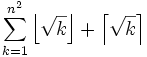$\sum_{k=1}^{n^2}{\left \lfloor \sqrt{k} \right \rfloor+ \left \lceil \sqrt{k} \right \rceil}$ for all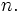 $n.\,$

Help from landen based on number crunching. Not sure if these help:

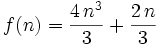
$f(n)={{4\,n^3}\over{3}}+{{2\,n}\over{3}}$

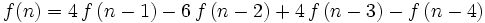
$f(n)=4\,f\left(n-1\right)-6\,f\left(n-2\right)+4\,f\left(n-3\right)-f \left(n-4\right)$

HiLander found a solution without these hints. Very clever.

Tuesday, 17th of April

posted by Crito

Source: Magnuz's Problem solving class.

Compare tan(sin x) and sin(tan x) for 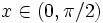$x \in (0, \pi/2)$ .

Thursday, 12th of April

posted by Crito

Find the number of positive integers $x < 10 2006$ such that $x 2 - x$ is divisible by $102006$ .

Solution by int-e.

Tuesday, 10th of April

posted by Crito

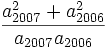Let a sequence be defined as follows: $a 1 = 3$ , $a 2 = 3$ , and for $n \ge 2, a_{n+1}a_{n-1}= a_{n}^{2}+2007$ . Find the largest integer less than or equal to $\frac{a_{2007}^{2}+a_{2006}^{2}}{a_{2007}a_{2006}}$ .

Solution by int-e

Retrieved from "http://efnet-math.org/w/POTD_2007-04"