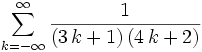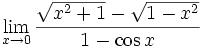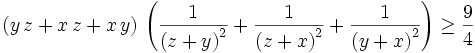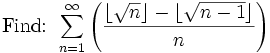POTD 2006-09
September 2006
Saturday, 30th of September
Today's POTDs courtesy of xkcd (http://xkcd.com/c135.html).
Friday, 29th of September
from Magnus-
Find a positive constant 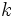 , such that
, such that 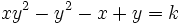 has precisely 3 solutions in positive integers.
has precisely 3 solutions in positive integers.
Solution by flamingsp: Click here (http://www.infimum.org/metadata/POTD-2006-09-29.pdf)
Wednesday, 27th of September
(1) Prove that no order can be defined in the complex field that turns it into an ordered field.
(2) If  is a metric on set
is a metric on set 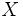 show that
show that 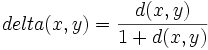 is also a metric on
is also a metric on 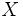 and that
and that 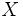 is bounded in terms of this metric. Do the two metrics
is bounded in terms of this metric. Do the two metrics  and
and 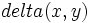 determine the same open subsets of
determine the same open subsets of 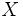 ? [Or Give a counter example]
? [Or Give a counter example]
Sunday, 24th of September
from Magnus-
Given 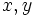 in positive integers. Determine the least value of
in positive integers. Determine the least value of 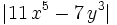
Saturday, 23rd of September
from Johnster via Kit
Let 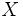 be a compact Hausdorff space and
be a compact Hausdorff space and 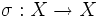 be a homeomorphism with no fixed points.
be a homeomorphism with no fixed points.
Let  be the ideal in generated by functions of the form
be the ideal in generated by functions of the form  . Show that
. Show that 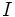 is dense in (and hence equal to)
is dense in (and hence equal to) 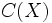 .
.
Not good enough at Topology? Here is a problem to attack with your computer algebra system skills.
from neobuddha via landen
Metal tanks are made by cutting rectangular squares out of the
corners of rectangular sheets of metal. Then the sides are folded up and
welded to form an open aquarium-shaped tank. The tank is to hold 10
cubic meters and the sheets can be gotten any size but they are 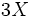 long and
long and 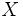 wide. What size sheets should be used so that the finished weight of the tanks is minimized.
wide. What size sheets should be used so that the finished weight of the tanks is minimized.
A variation on this problem is very common in Calc I. In the common variation the area of the uncut metal is to be minimized for a given volume. The problem above is only slightly different but is harder. landen got an exact symbolic answer but not by hand. Get out your favorite CAS.
Friday, 22nd of September
from A 1987 STEP paper via Kit
I'm not sure if this is actually a good question, but it's so utterly random that I had to post it.
My two friends, who shall remain nameless, but whom I shall refer to as P and Q, both told me this afternoon that there is a body in my fridge. I'm not sure what to make of this, because P tells the truth with a probability of only p, while Q (independently) tells the truth with probability q. I haven't looked in the fridge for some time, so if you had asked me this morning, I would have said that there was just as likely to be a body in it as not. Clearly, in view of what P and Q told me, I must revise this estimate. Explain carefully why my new estimate of the probability of there being a body in the fridge should be
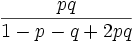
I have now been to look in the fridge, and there is indeed a body in it; perhaps more than one. It seems to me that only my enemy A, or my enemy B, or (with a bit of luck) both A and B could be in my fridge, and this evening I would have judged these three possibilities to be equally likely. But tonight I asked P and Q separately whether or not A was in the fridge, and they each said that he was. What should be my new estimate of the probability that both A and B are in my fridge?
Of course, I always tell the truth.
Tuesday, 19th of September
from fido7.ru.math via Inept
Let 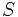 be a finite set with
be a finite set with 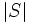 being a prime number. Let
being a prime number. Let 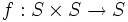 be a binary operation such that
be a binary operation such that  and
and 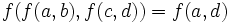 for any
for any  from
from 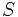 . Prove that either
. Prove that either 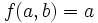 for all
for all 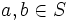 , or
, or 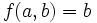 for all
for all 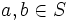 .
.
Solution (http://efnet-math.org/~david/POTD.pdf) by Kit. Solution by HiLander. Solution by koro
Sunday, 17th of September
From atomic by way of R^^n Find:
Solution (http://efnet-math.org/~david/POTDSep17.pdf) by Kit
Saturday, 16th of September
from stakked, by way of HiLander:
- Show that for every
![c \in [-1,1]](https://efnet-math.org/wiki/images/math/f92993f6a120105bff15774b2161dd3f.png) , there is an
, there is an 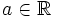 with
with 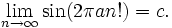
Hint: Consider the POTD from 9/4.
Friday, 15th of September
from cheater
- Prove:
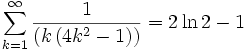
Solution (http://encyclomaniacs.sound-club.org/~fs/temp/POTD-2006-09-15.pdf) from flamingspinach
Wednesday, 13th of September
from Karlsen
- Show that
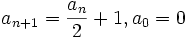 , converges, and find (and prove) a formula for
, converges, and find (and prove) a formula for 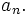
Solution (http://encyclomaniacs.sound-club.org/~fs/temp/POTD-2006-09-13.pdf) from flamingspinach
Tuesday, 12th of September
from scoobydew
Calc I students
Monday, 11th of September
from cheater
Rated fairly hard. Students without some analysis will probably have trouble.
Let 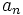 be a sequence of non-negative real numbers which satisfy
be a sequence of non-negative real numbers which satisfy
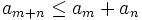
Show that
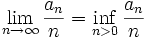
Solution by HiLander
Friday, 8th of September
Constructed by landen for Calc I Students. Please don't spoil in #math 'til Saturday UTC
Solution by binrapt. Multiple Solutions (http://kilian.byethost5.com/mytemp/potd_9_11_2006.pdf) by _kmh_
Thursday, 7th of September
From a HS Contest. landen solved it with common theorems so it isn't too hard. Show that for positive real numbers  :
:
Tuesday, 5th of September
From Polytope
Let 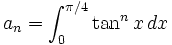 .
.
- Show that
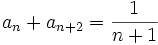 for all non-negative integers n.
for all non-negative integers n.
- Using this result, show that
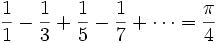 .
.
Monday, 4th of September
From Kit
Show that

Saturday, 2nd of September
From maks
- Prove that every real number is the sum of two Liouville numbers. (A Liouville number is an irrational number x such that, for every positive integer n, there exists a rational number p/q so that |x - p/q| < 1/q^n)
Friday, 1st of September
From evilgeek
Solution from Karlsen.