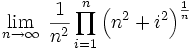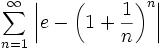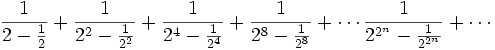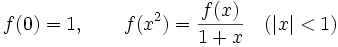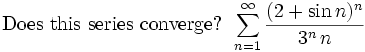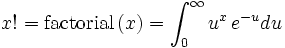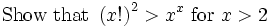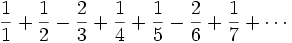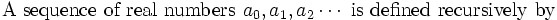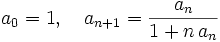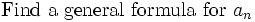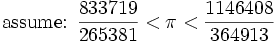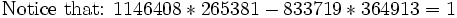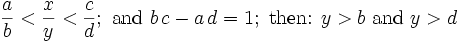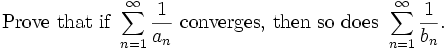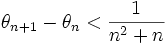POTD 2006-04

Table of contents
1 April 2006

1.1 Sunday, April 30
1.2 Saturday, April 29
1.3 Friday, April 28
1.4 Wednesday, Apr. 26
1.5 Monday, Apr. 24
1.6 Friday, Apr. 21
1.7 Monday, Apr. 17
1.8 Saturday, Apr. 15
1.9 Friday, Apr. 14
1.10 Wednesday, Apr. 12
1.11 Monday, Apr. 10
1.12 Saturday, Apr. 8
1.13 Thursday, Apr. 6
1.14 Wednesday, Apr. 5

April 2006

Sunday, April 30

Show off your Calc I skills: 1.

\lim_{n\rightarrow\infty}\;\frac{1}{n^2}\prod_{i=1}^n{\left(n^2+i^2\right)^{\frac{1}{n}}}

2. Does this sum converge:

\sum_{n=1}^{\infty}\, \left| e - \left(1+\frac{1}{n}\right)^{n}\right|

See how you did

Saturday, April 29

from Polytope

You have a perfect 12 hr analog clock. There is an hour hand, a minute hand and a sweep second hand. All the hands have a constant angular velocity. The hands are indistinguishable. Can you tell the time from a strobe photo of the clock?

Friday, April 28

Stolen from Anil's site (http://godel.princeton.edu/wiki/index.php/Main_Page)

Find exact value:

\int_0^1 \frac{\log(1+x)\,dx}{1+x^2}

landen solved this without contour integration but hopes someone can find a good contour. Solution

Bonus Problem, slightly easier and highly related:

Find exact value:

\int_0^{\pi}\log(\sin(x))\,dx

Wednesday, Apr. 26

Evaluate the sum:

\frac{1}{2-\frac{1}{2}}+\frac{1}{2^2-\frac{1}{2^2}}+ \frac{1}{2^4-\frac{1}{2^4}}+\frac{1}{2^8-\frac{1}{2^8}}+\cdots \frac{1}{2^{2^n}-\frac{1}{2^{2^n}}}+\cdots

Solution from landen

Monday, Apr. 24

Find, with proof, all functions f(x) which are defined for real numbers | x | < 1, continuous at x = 0, which satisfy:

f(0)=1,\qquad f(x^2)=\frac{f(x)}{1+x}\quad (|x|<1)

Friday, Apr. 21

from Rustem

Find all strictly increasing, multiplicative functions

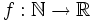
f:\mathbb{N}\to\mathbb{R}
(multiplicative here means: f(mn) = f(m) * f(n) when gcd(m,n) = 1)

Bonus Problem

from landen

\mbox{Does this series converge? }\sum_{n=1}^{\infty}\frac{(2+\sin n)^n}{3^n\,n}

landen plans to attack with continued fractions and irrationality of π. Maybe there is a cute answer. Attack failed. This is a toughie.

Monday, Apr. 17

from ddeerr

Define for positive, real x, not just integers:

x!=\mathrm{factorial}\,(x)=\int_0^\infty u^x\,e^{-u}du
\mbox{Show that }\left(x!\right)^2 > x^x \mbox{ for }x>2\,

Solution

Saturday, Apr. 15

from landen

a_1=\sqrt{2},\ a_2=\sqrt{2}^\sqrt{2},\cdots,\ a_7=\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^\sqrt{2}}}}}},\cdots

\mbox{Show that the limit }a_\infty\mbox{ exists and find its value.}

Friday, Apr. 14

from landen

Prove that the series

\frac{1}{1}+\frac{1}{2}-\frac{2}{3}+\frac{1}{4}+\frac{1}{5}-\frac{2}{6}+\frac{1}{7}+\cdots

converges and find its limit. Solution by landen

Wednesday, Apr. 12

from landen

\mbox{A sequence of real numbers }a_0,a_1,a_2\cdots\mbox{ is defined recursively by}
a_0=1,\quad a_{n+1}=\frac{a_n}{1+n\,a_n}
\mbox{Find a general formula for }a_n\,

Monday, Apr. 10

from landen

\mbox{assume: }\frac{833719}{265381} < \pi < \frac{1146408}{364913}
\mbox{Notice that: }1146408*265381-833719*364913 = 1\,

Use this to show that any better rational approximation to π requires a larger denominator.

Hint: Show that if three positive rational numbers have

\frac{a}{b}<\frac{x}{y}<\frac{c}{d};\mbox{ and }b\,c-a\,d = 1;\mbox{ then: }y>b\mbox{ and }y>d

Saturday, Apr. 8

Rated easy.

Each point in the plane is colored either orange or blue. Prove that one of these colors contains, for each positive value of d, a pair of points at distance d.

Thursday, Apr. 6

landen doesn't know how hard it is.

\mbox{Let }a_1,\,a_2, \cdots\mbox{ be a sequence of positive real numbers,}
\mbox{and let }b_n\mbox{ be the arithmetic mean of } a_1, \,a_2, \cdots, a_n.
\mbox{Prove that if }\sum_{n=1}^\infty\frac{1}{a_n}\mbox{ converges, then so does }\sum_{n=1}^\infty\frac{1}{b_n}.

Wednesday, Apr. 5

landen rated: fairly easy, first idea worked.

\mbox{Let }\theta_n = \arctan(n)\mbox{. Prove that, for } n = 1,2,3,\cdots\,
\theta_{n+1}-\theta_n < \frac{1}{n^2+n}

solution

Retrieved from "http://efnet-math.org/w/POTD_2006-04"