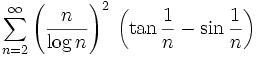POTD 2006-10

Table of contents

1 October 2006

1.1 Tuesday, 31st of October
1.2 Monday, 16th of October
1.3 Sunday, 15th of October
1.4 Saturday, 14th of October
1.5 Friday, 13th of October
1.6 Thursday, 12th of October
1.7 Wednesday, 11th of October
1.8 Tuesday, 10th of October
1.9 Saturday, 7th of October
1.10 Wednesday, 4th of October

October 2006

Tuesday, 31st of October

from evilthang

Prove whether the following converges or diverges.

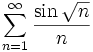
$\sum_{n=1}^{\infty }{{{\sin \sqrt{n}}\over{n}}}$

Solution by landen.

Monday, 16th of October

from Crito

(Source: various places)

1. Let 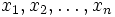$x_1,x_2,\ldots,x_n$ be real numbers. Prove that

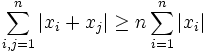
$\sum_{i,j=1}^n |x_i+x_j|\geq n\sum_{i=1}^n |x_i|$

Solution (http://int-e.home.tlink.de/math/prob1016_1.pdf) by int-e

2. Suppose that p is a prime number. Find all natural numbers n such that 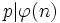$p|\varphi(n)$ and for all a such that (a,n)=1 we have

$n|a^{\frac{\varphi(n)}{p}}-1$

3. Find all nonnegative integer solutions (x,y,z,w) of the equation

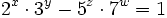$2^x\cdot3^y-5^z\cdot7^w=1$ .

4. The sequence ${a n}$ is defined by: 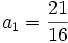$a_1=\frac{21}{16}$ , and for $n\ge2$ ,

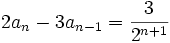$2a_n-3a_{n-1}=\frac{3}{2^{n+1}}$ .

Let m be an integer with 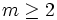$m\ge2$ . Prove that: for 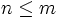$n\le m$ , we have

$\left(a_n+\frac{3}{2^{n+3}}\right)^{\frac{1}{m}}\left(m-\left(\frac{2}{3}\right)^{{\frac{n(m-1)}{m}}}\right)<\frac{m^2-1}{m-n+1}$ .

5. Find all (x,y,z) positive integers, such that: 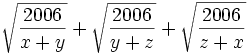$\sqrt{\frac{2006}{x+y}} + \sqrt{\frac{2006}{y+z}} + \sqrt{\frac{2006}{z+x}}$ , is an integer.

Solution (http://int-e.home.tlink.de/math/prob1016_5.pdf) by int-e.

6. Find all ordered triples (a,b,c) of positive integers such that $a b c + a b + c = a 3$

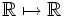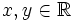7. Find all functions f : $\mathbb{R} \mapsto \mathbb{R}$ such that $f (x y + f (x)) = x f (y) + f (x)$ for all $x,y \in \mathbb{R}$ .

8. Find all positive integers n that can be uniquely expressed as a sum of five or fewer squares.

9. Provide a natural number n > 3 and positive real numbers $x 1, x 2 ..., x n$ , whose product is 1. Prove the inequality:

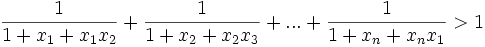$\frac{1}{1 + x_1 + x_1x_2} + \frac{1}{1 + x_2 + x_2x_3} +... + \frac{1}{1 + x_n + x_nx_1} > 1$ .

Solution (http://int-e.home.tlink.de/math/prob1016_9.pdf) by int-e.

Sunday, 15th of October

From zeno (due to Ron Rivest)

Say you have a burnable CD-like device with n bit-points on it, where an unused/unburned point means 0 and a hole burned there means 1, and once burned, a hole can't be changed back. Devise a simple data representation scheme so that you can burn a representation of ANY bitstring of length 2N/3 on it, and you can then burn another such image over that by only burning new points (only on unburned points from the first image), in such a way that the same data-reading method works on both images perfectly.

Saturday, 14th of October

From Neverwher via Kit

Let 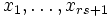$x_1, \ldots, x_{rs + 1}$ be a sequence of numbers. Show that it has an increasing subsequence of length $r + 1$ or a decreasing one of length $s + 1$ .

Solution via HiLander

Friday, 13th of October

by Crito

Find the biggest real number 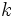$k\,$ that for each right-angled triangle with sides $a,b,c\,$ :

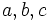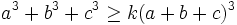
$a^{3}+b^{3}+c^{3}\geq k(a+b+c)^{3}$

Solution by landen

II.

from Iran NMO 2006 , corrected :

For positive numbers 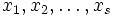$x_{1},x_{2},\dots,x_{s}$ , we know that 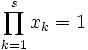$\prod_{k=1}^{s}x_{k}=1$ . Prove that for each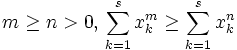 $m\geq n>0,\, \sum_{k=1}^{s}x_{k}^{m}\geq\sum_{k=1}^{s}x_{k}^{n}$

Solution by landen

Thursday, 12th of October

from landen

Probably not hard or advanced.

$[a_1,\,a_2,\,\cdots ]$ is an infinite arithmetic sequence of positive integers. Show if it contains a perfect square it contains infinitely many perfect squares.

Solution (http://encyclomaniacs.sound-club.org/~fs/math/POTD-2006-10-12.pdf) by flamingspinach

Wednesday, 11th of October

from landen

This problem can be solved by very elementary means, or you can use Maple or something on it to help. Also, it can be blown away with some theorems in algebraic number theory and abstract algebral

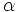$\alpha\,$ is a real root of 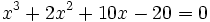$x^3 + 2x^2 + 10x - 20 = 0\,$ . Show that 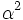$\alpha ^2\,$ is irrational.

Solutions by landen and Polytope

Tuesday, 10th of October

from Dudeney (1847-1930) classic problem

Three countrymen met at a cattle market. "Look here, " said Hodge to Jakes, "I'll give you six of my pigs for one of your horses, and then you'll have twice as many animals here as I've got." "If that's your way of doing business," said Durrant to Hodge, "I'll give you fourteen of my sheep for a horse, and then you'll have three times as many animals as I." "Well, I'll go better than that, " said Jakes to Durrant; "I'll give you four cows for a horse, and then you'll have six times as many animals as I've got here."

No doubt this was a very primitive way of bartering animals, but it is an interesting little puzzle to discover just how many animals Jakes, Hodge and Durrant must have taken to the cattle market.

Saturday, 7th of October

from koro.

Let $X$ and $Y$ be locally compact separable metric spaces. Given a continuous surjection 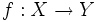$f:X\to Y$ , call a point 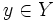$y \in Y$ a regular value of $f$ if for all $x\in f^{-1}(y)$ , f maps neighborhoods of $x$ to neighborhoods of $y$ . Prove the following topological version of Sard's theorem: For any such function, the set of regular values is residual in $Y$ (i.e. it contains a countable intersection of dense open sets).

Wednesday, 4th of October

from landen. Does this series converge? $\sum_{n=2}^{\infty}\left( \frac {n}{\log n}\right)^2\,\left(\tan \frac{1}{n}- \sin \frac{1}{n}\right)$

Retrieved from "http://efnet-math.org/w/POTD_2006-10"