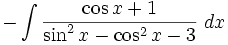POTD 2006-11
| Table of contents |
November 2006
Thursday, 30th of November
from Crito
Let  and
and 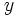 be positive integers such that
be positive integers such that 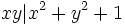 . Show that
. Show that 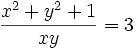
Wednesday, 22nd of November
from dedekind
Let 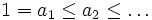 and aman = amn. Prove that either an = 1 for all n, or an = n1 / p for some p > 0.
and aman = amn. Prove that either an = 1 for all n, or an = n1 / p for some p > 0.
Solution by Kit
Thursday, 16th of November
Show that 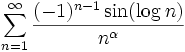 converges iff
converges iff 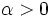 .
.
Solution by landen by famous secret method.
Saturday, 11th of November
from Crito
1. 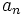 is a sequence that
is a sequence that 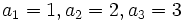 , and
, and
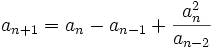 Prove that for each natural
Prove that for each natural  ,
, 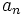 is integer.
is integer.
2. Let  and
and  be positive integers such that
be positive integers such that 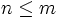 . Prove that
. Prove that
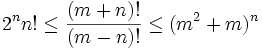
3. For positive 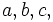
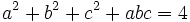 Prove
Prove 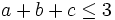
4.  and for
and for 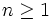 we know that :
we know that : 
 is an even number, and
is an even number, and 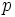 is prime number such that
is prime number such that 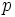 divides
divides 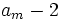 . Prove that
. Prove that 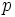 divides
divides 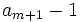 .
.
5. π(n) is the number of primes that are not bigger than n. For  we have π(n) | n. Do there exist infinitely many integers n that π(n) | n?
we have π(n) | n. Do there exist infinitely many integers n that π(n) | n?
Friday, 10th of November
from Kit
Let X be a separable topological space, and C(X) the space of continuous functions from X to 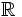 with the product topology. Show that compact subsets of C(X) are metrizable.
with the product topology. Show that compact subsets of C(X) are metrizable.
Tuesday, 7th of November
from yoel and landen; may be very hard
Empirical evidence is that the following limit is 1. What can you find out about it?

Sunday, 5th of November
from i_c-Y
Evaluate:
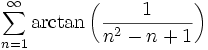
Solution by landen and int-e
Saturday, 4th of November
from #math honours calc sorry, no knighthood for this one.

Friday, 3rd of November
from #math honours calc II with knighthood