POTD 2006-12
December 2006
Saturday, 30th of December
edited by landen
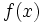 and
and 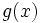 are real valued functions defined on all of
are real valued functions defined on all of 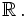
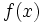 is not always 0.
is not always 0. 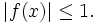
For all 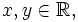

Show that 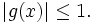
Solution by i_c-Y
Friday, 29th of December
suggested by landen
{ak} is a sequence of distinct positive integers. Prove that for all positive integers 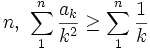
Solution (http://encyclomaniacs.sound-club.org/~fs/math/POTD-2006-12-29.pdf) by flamingsp
Thursday, 28th of December
from Crito
If 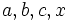 are real numbers such that
are real numbers such that 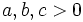 and
and 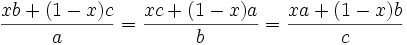 , then prove that
, then prove that  .
.
Solution by int-e.
Monday, 25th of December
from Crito
Find all non-negative integers m,n,p,q such that pm * qn = (p + q)2 + 1.
Sunday, 24th of December
from landen for ziggggggy and i_c-Y
1. Find the general solution:
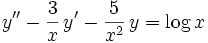
Hint: notice 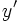 is divided by
is divided by  and
and 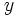 is divided by
is divided by 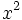 so you get
so you get 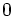 when added to
when added to 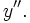 Think of a super common type of function where that might happen.
Think of a super common type of function where that might happen.
2. Solve your favorite:
a. 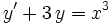
b. 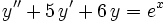
c. 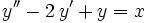
d. 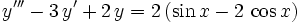
Saturday, 23rd of December
posted by landen
The positive integers 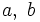 are such that
are such that 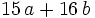 and
and 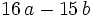 are both squares of positive integers. What is the least possible value
that can be taken on by the smaller of these two squares?
are both squares of positive integers. What is the least possible value
that can be taken on by the smaller of these two squares?
Wednesday, 20th of December
from Crito
Suppose that m and n are odd integers such that m2 − n2 + 1 divides n2 − 1. Prove that m2 − n2 + 1 is a perfect square.
Tuesday, 19th of December
from ermular
1. Find: 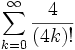
Solution by landen. Other solution by Kit.
Saturday, 16th of December
from Kit
1. Let V be a normed space, 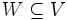 a closed subspace. Fix t > 0 and let
a closed subspace. Fix t > 0 and let 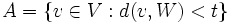 .
.
Show there is a continuous function 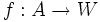 with
with 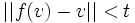
Not particularly hard, but might require some advanced knowledge.
from Crito
2. Prove that the equation 6(6a2 + 3b2 + c2) = 5n2 has no solutions in integers except a = b = c = n = 0. Solution by int-e.
3. Let a, b, c be the lengths of the sides of a triangle. Prove that
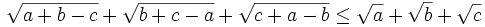
and determine when equality occurs. Solution by landen.
Friday, 15th of December
from Koro
1) Find a non-measurable subset of the plane such that all its vertical and horizontal sections are measurable.
2) Can you find it such that all vertical and horizontal sections consist of a single point?
Friday, 8th of December
from Polytope
Please do not solve in the channel before Dec 10 if you have had real analysis. This is for smart Calc students.
Let 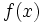 be a function of a real variable with real values.
be a function of a real variable with real values.
If  is irrational then
is irrational then 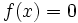
If  is rational
is rational 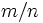 in lowest terms,
in lowest terms, 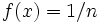
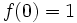
Show that 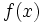 is nowhere differentiable.
is nowhere differentiable.
Solution from landen
Solution from hilander
from Crito
Source: <insert-some-strange-corners-of-the-web-here>
Prove that 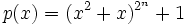 is irreducible in
is irreducible in ![\mathbb Z[x]](https://efnet-math.org/wiki/images/math/3182ba9f80992f4f3bf853027b5dc2a3.png)
Solution (http://www.efnet-math.org/math_tech/BonusProbDec0806.pdf) by hochs.