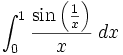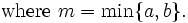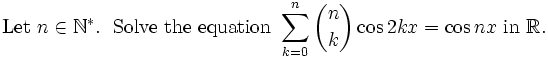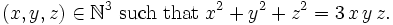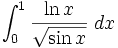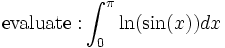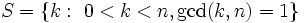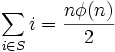POTD 2006-03

Table of contents

1 March 2006

1.1 Wednesday, Mar. 29
1.2 Sunday, Mar. 26
1.3 Saturday, Mar. 25
1.4 Friday, Mar. 24
1.5 Thursday, Mar. 23
1.6 Tuesday, Mar. 21
1.7 Saturday, Mar. 18
1.8 Friday, Mar. 17, 2006
1.9 Thursday, Mar. 16, 2006
1.10 Wednesday, Mar. 15, 2006
1.11 Sunday, Mar. 12, 2006
1.12 Friday, Mar. 10, 2006
1.13 Thursday, Mar. 9, 2006
1.14 Monday, Mar. 6, 2006
1.15 Sunday, Mar. 5, 2006
1.16 Friday, Mar. 3, 2006
1.17 Thursday, Mar. 2, 2006
1.18 Wednesday, Mar. 1, 2006

March 2006

Wednesday, Mar. 29

from landen

Evaluate numerically with error bounds to a bunch of decimals if you can:

$\int_{0}^{\infty }{{{\sin \left(\pi\,x\right)}\over{\log\left(x \right)}}\;dx}$

Solution by landen. The solution has a Pari program for experimenting and was more work than landen intended when he posed the problem.

Sunday, Mar. 26

from Anil

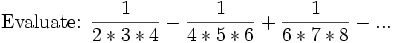
$\mbox{Evaluate: }\frac{1}{2*3*4} - \frac{1}{4*5*6} + \frac{1}{6*7*8} - ...$

Two different solutions

Saturday, Mar. 25

from bhargav

If $2 n + 1$ and $3 n + 1$ are squares, $n$ is divisible by 40.

solution

Friday, Mar. 24

from landen

Show this integral converges:

$\int_{0}^{1}{{{\sin \left({{1}\over{x}}\right)}\over{x}}\;dx}$

Can you get a numerical approximation of the value to a bunch of decimal places?

Solution

Thursday, Mar. 23

from Anil

$\mathrm{Prove\ that:\ }\mathrm \sum_{i=0}^m \binom{x+y+i}{i}\binom{y}{a-i}\binom{x}{b-i}=\binom{x+a}{b}\binom{y+b}{a} ,$

$\mathrm{where\ }m=\min\{a,b\}.\,$

Tuesday, Mar. 21

from Anil

$\mathrm{Let\ }n\in\mathbb{N}^* .\mathrm{\ \ Solve\ the\ equation\ }\sum_{k=0}^n {n \choose k}\cos2kx=\cos nx\mathrm{\ in\ }\mathbb{R}.\,$

solution by landen.

Saturday, Mar. 18

from Kit

Let $V$ be a vector subspace of $L 2 ([0,1])$ such that there is a constant $K$ so that for any 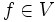$f \in V$ we have $\forall x \in [0, 1] \ |f(x)| \leq K ||f||_2$ . Show that the dimension of $V$ (as a vector space) is at most $K 2$ .

Friday, Mar. 17, 2006

from Anil Show that there exist infinitely many triples:

$(x,y,z) \in \mathbb{N}^3 \mathrm{\ such\ that\ }x^2+y^2+z^2=3\,x\,y\,z.$

Thursday, Mar. 16, 2006

From landen Prove this integral converges:

$\int_{0}^{1}{{{\ln x}\over{\sqrt{\sin x}}}\;dx}$

Then for real fun use a computer or your favorite calculator to estimate the integral to a bunch of decimal places. See how many you can do and if you can tell how accurate your answer is. Solution by landen and Galois.

Wednesday, Mar. 15, 2006

Show $1 + x + \cdots + x^{n-1}$ is irreducible over Z/2 iff $n$ is prime and 2 is a primitive root mod $n$ . [Harder than easy.]

Sunday, Mar. 12, 2006

from landen

$\mathrm{evaluate: }\int_0^\pi \ln(\sin(x))dx$

There is no closed form antiderivative, be clever. Definite integration techniques are required.

Friday, Mar. 10, 2006

from dedekind rated: needs no advanced math

Find all $n$ such that $2 n$ divides $3 n - 1$ .

solution being edited

from Karlsen

Let $a$ and $n$ be positive integers. Suppose that $n | (a - 1) 2006$ .

Show that $n | (1 + a + .. + a n - 1)$ .

Thursday, Mar. 9, 2006

Please do not give a solution in #math until evening of March 9.

Show that in positive integers, $\mathbb{Z}^+$ :

$S=\{k:\ 0<k<n, \mathrm{gcd}(k,n)=1\}\,$

$\sum_{i\in S}i=\frac{n\phi(n)}{2}$

$φ(n)$ is Euler's $φ$ function (http://en.wikipedia.org/wiki/Euler's_totient_function), the number of numbers less than $n$ and relatively prime to $n$ .

$\phi(n)=|S|\,$

Hint: No deep theorems or familiarity with $φ(n)$ is need.

Monday, Mar. 6, 2006

from Anil

Prove that for every positive integer $n$ there exists a unique ordered pair $(a, b)$ of positive integers such that

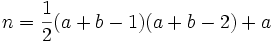
$n = \frac{1}{2}(a + b - 1)(a + b - 2) + a$

Many people solved this. The following is landen's writeup of the solution of saetji.

Sunday, Mar. 5, 2006

From Kit

Let 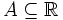$A \subseteq \mathbb{R}$ be closed. Show that there is a sequence $(x n)$ such that $A = {a : a$ is the limit of a subsequence of $x n}$ .

Bonus question: If $A$ is non-empty, can you choose $(x n)$ to lie entirely in $A$ ?

from meru

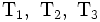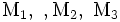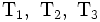In a triangle with no special properties the inscribed circle touches the triangle at $\mathrm{T_1, \ T_2, \ T_3}$ . The centers of each side are at $\mathrm{M_1,\ ,M_2,\ M_3}$ . The bisectors of the angles of the triangle pass thru the center of the circle $I$ . The points $\mathrm{S_1, \ S_2, \ S_3}$ are the reflections of $\mathrm{T_1, \ T_2, \ T_3}$ thru the associate angle bisector.

The lines 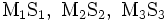$\mathrm{M_1S_1, \ M_2S_2, \ M_3S_3}$ appear to intersect at a common point. Prove this.

Friday, Mar. 3, 2006

from yannick

a. Show that 2005 can be written as a sum of squares in 2 ways.

b. bonus: When is the next year that can be written as a sum of squares in even 1 way?

A REAL MATH PROBLEM from Anil

c. Prove that, for all natural numbers $n$ , $2 2 n + 24 n - 10$ is divisible by 18.

solution from landen

Thursday, Mar. 2, 2006

from Anil

Show that n can be taken so large that 1 + (1/2) + (1/3) + .... + (1/n) > 100

Wednesday, Mar. 1, 2006

from Anil

Easy: How many ordered triples $[x, y, z]$ of positive integers satisfy $x y z$ = 4000.

Retrieved from "http://efnet-math.org/w/POTD_2006-03"