POTD 2007-03

Table of contents

1 March 2007

1.1 Friday, 30th of March
1.2 Tuesday, 27th of March
1.3 Sunday, 25th of March
1.4 Tuesday, 20th of March
1.5 Sunday, 18th of March
1.6 Monday, 12th of March
1.7 Sunday, 4th of March
1.8 Saturday, 3rd of March
1.9 Thursday, 1st of March

March 2007

Friday, 30th of March

Safrole

Let 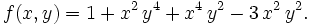$f(x,y) = 1 + x^{2}\,y^{4}+x^{4}\,y^{2}-3\,x^{2}\,y^{2}.$

Determine whether there exist polynomials $g i (x, y)$ with real coefficients such that

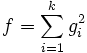$f = \sum_{i=1}^{k}g_{i}^{2}\,$ or argue that such a representation is not possible.

Solution by int-e.

Tuesday, 27th of March

Anil

Prove that for each 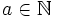$a\in\mathbb N$ , there are infinitely many natural n, such that $n | a n - a + 1 - 1$

Solution by int-e.

Sunday, 25th of March

Crito from an Iranian Math competition

Let 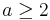$a\geq 2$ be a natural number. Prove that 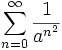$\sum_{n=0}^\infty\frac1{a^{n^{2}}}$ is irrational.

Solution by HiLander.

Tuesday, 20th of March

Crito -- Put Landen's skills on inequalities to test.

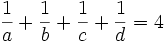
$a, b, c, d$ are positive real numbers satisfying the following condition: $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}=4$

Prove that: $\sqrt[3]{\frac{a^{3}+b^{3}}{2}}+\sqrt[3]{\frac{b^{3}+c^{3}}{2}}+\sqrt[3]{\frac{c^{3}+d^{3}}{2}}+\sqrt[3]{\frac{d^{3}+a^{3}}{2}}\leq 2(a+b+c+d)-4$

Solution by int-e.

Sunday, 18th of March

Crito from a land far far away.

a, b, c, d are positive integers and $a d = b 2 + b c + c 2$

Prove that $a 2 + b 2 + c 2 + d 2$ is a composite number.

Solution by int-e

Monday, 12th of March

Polytope

Prove the Batman Integral (http://rofl.wheresthebeef.co.uk/batman-calc.jpg).

Sunday, 4th of March

Flamingsp(inach)

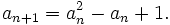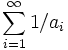Let $a 1 > 0$ , and $a_{n+1} = a_n^2 - a_n + 1.$ Find $\sum_{i=1}^\infty 1/a_i$ .

Saturday, 3rd of March

Crito

Prove that there exist no 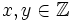$x,y \in \mathbb{Z}$ such that $y 2 = x 3 + 23$

Solution (http://www.ma.ic.ac.uk/~acorti/teaching/hmwk3_06.pdf) Scroll down to problem 10.

Solution by landen and int-e.

Thursday, 1st of March

For all integers 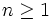$n\geq 1$ we define 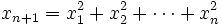$x_{n+1}=x_1^2+x_2^2+\cdots +x_n^2$ , where $x 1$ is a positive integer. Find the least $x 1$ such that 2006 divides $x 2006$ .

Solution by int-e.

Retrieved from "http://efnet-math.org/w/POTD_2007-03"