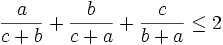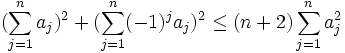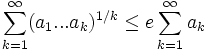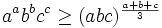POTD 2006-02

This is the Problem of the Day section for February 2006.

The problems are shown in reverse order.

Table of contents

1 Tuesday, Feb. 28, 2006

2 Sunday, Feb. 26, 2006

3 Saturday, Feb. 25, 2006

4 Thursday, Feb. 23, 2006

5 Wednesday, Feb. 22, 2006

6 Monday, Feb. 20, 2006

7 Thursday, Feb. 16, 2006

8 Tuesday, Feb 14, 2006

9 Monday, Feb 13, 2006

10 Saturday, Feb 11, 2006

11 Friday, Feb 10, 2006

12 Wednesday, Feb 8, 2006

13 Thursday, Feb 2, 2006

Tuesday, Feb. 28, 2006

from Anil

Find all primes $p$ , $q$ and even $n$ > 2 such that $p n + p n - 1 + ... + p + 1 = q 2 + q + 1$ .

Solution by HiLander

Sunday, Feb. 26, 2006

from landen If $a$ , $b$ , and $c$ are the sides of a nondegenerate triangle then

${{a}\over{c+b}}+{{b}\over{c+a}}+{{c}\over{b+a}}\leq 2$

Clever solution

Saturday, Feb. 25, 2006

from Karlsen Show that

$(\sum_{j=1}^n a_j)^2 + (\sum_{j=1}^n (-1)^j a_j)^2 \le (n+2)\sum_{j=1}^n a_j^2$

Can you improve upon (n+2)?

bonus problem: show for $a, b, c > 0$ :

$\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\ge \frac{3}{2}$

solution from landen

Thursday, Feb. 23, 2006

from Karlsen

Prove that:

$\sum_{k=1}^{\infty}(a_1...a_k)^{1/k} \le e\sum_{k=1}^{\infty}a_k$

note from landen: This is Carleman's inequality. This paper (http://jipam-old.vu.edu.au/v4n3/135_02_www.pdf) has several proofs.

Wednesday, Feb. 22, 2006

from Karlsen

Show that if $a, b, c > 0$ then

$a^a b^b c^c \ge (abc)^{\frac{a+b+c}{3}}$

Short solution by argz

Solution by landen

HiLander solved the same inequality for n variables instead of just three. General solution by HiLander (http://www.efnet-math.org/math_tech/abc.pdf). landen shortened HiLander's solution to make a quick read solution.

(Note from HiLander: landen's solution generalizes to the n variable case with very little effort, and has the benefit of being noticeably more clever than my own. And argz's solution generalizes much faster, and looks much prettier. )

Monday, Feb. 20, 2006

from Anil

The sum of a certain number of consecutive positive intergers is $1000$ . Find the integers. Solution by landen

Thursday, Feb. 16, 2006

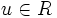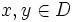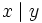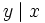(College Mathematics Journal Vol. 37 No. 1 Jan. 2006) Two elements $x, y$ in a commutative ring $R$ are said to be associates if there exists a unit $u \in R$ such that $x = u y$ . Show that there exists a commutative ring $D$ (with identity) and elements $x,y \in D$ such that $x \mid y$ and $y \mid x$ , but $x$ and $y$ are not associates.

Solution: dvi (http://jgarrett.org/math/problem820.dvi) pdf (http://jgarrett.org/math/problem820.pdf)

Tuesday, Feb 14, 2006

from Anil

[my valentine's day gift for you all ;)]

Show that $a 2 + b 2 + c 2 = (a - b)(b - c)(c - a)$ has infinitely many integral solutions.

Below are some of the integral solutions computed by brute force. The problem has been solved by Arne Smeets and independently by Inept. There is a discussion of their Solution by landen

a b c

0 1 -1

14 21 7

100 125 75

250 265 155

266 497 259

330 385 275

Monday, Feb 13, 2006

from Anil

Find all integers m, n such that (5 + 3 sqrt(2))^m = (3 + 5 sqrt(2))^n. Solution by landen

Saturday, Feb 11, 2006

from Anil. Solved by landen. Rated pre-calc, very easy. Symmetric Polynomials (http://www.cs.berkeley.edu/~oholtz/H90/equations.pdf) are overkill on this problem but they are worth learning about and are cool. Many math contests have symmetric polynomial problems.

Solve for integers x, y, z:

$x + y = 1 - z$

$x 3 + y 3 = 1 - z 3$

Friday, Feb 10, 2006

from Anil. For precalc students or maybe freshpersons.

if $x 5 - x 3 + x = a$ then, prove that 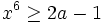$x^6 \geq 2a - 1$

Wednesday, Feb 8, 2006

from Anil

Find all pairs (a, b) of positive integers that satisfy (a^b)^2 = b^a. landen thought this problem was hard and got a version of this hint from Polytope.

Thursday, Feb 2, 2006

Prove by induction that (2n)!/(n!)^2 < (4^n)/sqrt(3n+1) for all n>1.

Retrieved from "http://efnet-math.org/w/POTD_2006-02"